機床主軸溫度測點的 K-means 優化及試驗
2020-4-10 來源:南通大學機械工程 南通第五機床 作者:周成 莊麗陽 袁江 高傳耀
摘要:針對機床熱誤差補償技術中溫度測點的優化選擇,提出一種基于 K-means 算法和 Pearson 相關系數相結合的方法。通過 K-means 算法將不同位置測點的溫度進行聚類,用 Pearson 相關系數計算溫度與主軸熱誤差之間的相關性,從每一類別中選出一個最優測點組成最優測點組合,并對最優測點處的結果進行熱誤差建模。在立式加工中心 VMC850E上對該方法進行了試驗驗證,將溫度測點的數量由 8 個減少至 2 個。經方差分析和 F 檢驗,驗證了最優測點處的溫度與熱變形之間顯著線性,模型可靠。
關鍵詞:主軸;K-means 算法;Pearson 相關系數;測點優化
1 、引言
在實際生產過程中,機床零部件的發熱最終會導致主軸在軸向產生偏移,對產品的加工精度造成影響,甚至產生報廢品[1-2]。大量研究表明,機床熱誤差已經取代幾何誤差,成為最主的誤差源,減小熱誤差已經成為企業亟待解決的問題之一。熱誤差補償技術相比機床結構改進,是減小熱誤差、提高加工精度的更加有效、經濟的方法。而溫度測點的優化布置是實現熱誤差補償的重點,其優化結果的有效性大大影響著熱誤差補償的精度[3-4]。近年來,國內外學者提出了熱誤差模態分析法、逐步線性回歸法、模糊聚類法、神經網絡法[5-7]等多種溫度測點的優化布置方法。但上述測點優化布置方法有的過程簡單,但十分不準確,影響熱誤差模型的準確性;有的過程十分復雜,而且需要大量的樣本,耗費大量的時間和成本,從而限制了這些方法在熱誤差建模與補償中的應用。
K-means 聚類是一種經典算法,其擁有效率高,分類明顯,能對大量數據進行分割聚類等特點。該算法通過不斷尋找新的聚類中心,使得聚類效果評價函數 J 不斷收斂,直至聚類不再變化,達到較優的聚類效果。將其與 Pearson 相關系數相結合,對機床主軸溫度測點進行優化。該法在對機床主軸進行熱態特性分析的基礎上,采用 K-means 算法對熱敏區域測點的溫度特征聚類,再通過 Pearson 相關系數選出與熱變形相關性最大的測點,實現主軸溫度測點優化。最后,對最優溫度測點進行熱誤差建模,并利用方差分析和 F 檢驗驗證模型的可靠性。
2、 溫度測點優化
2.1 熱態特性分析
在將主軸導入 ANSYS Workbench 進行熱態特性分析之前,為減小分析處理時龐大的計算量,需要對主軸結構進行合理簡化,簡化有如下幾點:
(1)去除一些對模型熱特性影響較小的特征(如倒角、小孔等);
(2)主軸及箱體結構中的一些腰型孔、小通孔、螺紋孔等均按實體處理;
(3)打刀缸及其附屬部件不在分析范圍內;
(4)主軸上的小配件不在模型中顯示。
完成主軸模型的簡化后,根據所選機床的實際情況,確定熱態特性分析的主體為主軸以及主軸箱。主軸的熱傳遞方式包括熱傳導、熱對流以及熱輻射。而此款立式加工中心主軸在冷卻液等的作用下,溫升較小,故忽略通過熱輻射失去的熱量,熱傳遞方式只考慮熱傳導和熱對流。其中,熱傳導系數由主軸及箱體的材料決定,而熱對流主要考慮套筒內冷卻液的強迫對流換熱、主軸旋轉帶動周圍空氣的流動形成的強迫對流換熱以及空氣的自然對流。由此可計算得主軸的熱邊界參數[8-10],如表 1 所示。
表 1 主軸熱邊界參數

將上述已知參數在有限元分析軟件中進行設定,并進行溫度場仿真,通過穩態熱分析結果劃定出具體的熱敏區域。主軸及箱體系統的穩態熱分析結果,如圖 1 所示。根據仿真結果,得知穩定后主軸最高溫度位于前端軸承,約為 32.9℃,其次為后端軸承,約為 30.3℃,即熱敏區域為前后軸承之間的區域。利用該軟件中的 Probe 探針,結合實際尺寸,初步確定熱敏區域范圍為[88mm,265mm]。

圖 1 主軸熱敏分析圖
2.2 K- me a ns 算法溫度聚類分析
K-means 聚類算法是一種基于劃分法的聚類算法,它將聚類溫度集內的所有溫度樣本的均值作為該聚類的中心點。其工作原理是首先從溫度測點集合中隨機選取 k 個溫度測點作為初始聚類中心,分別計算各個溫度測點到初始聚類中心的相似度(以歐式距離作為相似度測量準則),并根據計算所得的距離將每個溫度測點賦給最近的聚類中心。然后再計算該溫度測點集合內的所有溫度的平均值,得到新的聚類中心。反復循環計算,一旦連續兩次循環得到的聚類中心均為同一個溫度測點,說明溫度聚類分析完成。通常采用平方誤差函數 J 作為聚類效果的評價函數,公式如下:

式中:P—溫度分類 Cj中任一個溫度測點;Z—溫度分類 Cj的溫度聚類中心
算法流程如下:
(1)參數設定。隨機選擇 k 個溫度測點作為初始溫度聚類的中心;
(2)初始聚類。計算并比較溫度測點到每一個溫度聚類中心的距離,并根據最短距離聚類;
(3)修正聚類。根據新的溫度聚類,計算該溫度聚類的平均值;
(4)聚類結果。若溫度聚類中心未發生變化,輸出最終聚類結果,循環結束,否則,返回步驟(2)繼續迭代。
2.3 相關性分析
相關性分析是用來研究變量間關聯程度的一種統計方法,采用相關系數來表征。這里通過比較溫度測點與熱誤差之間的Pearson 相關系數,來選出溫度聚類結果中每一類別里的最優測點。相關系數 r 越大,則表明兩者間相關性越強。公式如下:
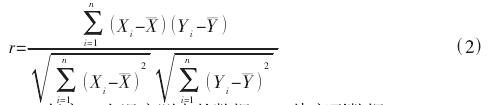
式中:X-任意有個溫度測點的數據;Y-熱變形數據。
3 、試驗驗證
3.1 實驗方案
以 VMC850E 高速高精密立式加工中心的主軸作為實驗對象,如圖 2 所示。在前端軸承與后端軸承之間的熱敏區域,均勻布置 8 個溫度傳感器,并在主軸軸向延長線上布置一個激光位移傳感器。采集數據時,8 個溫度傳感器分別將采集的溫度信息和標簽信息打包無線發送給讀寫器,上位機通過自編的 LabVIEW 串口調試程序接收溫度信息和標簽信息,實現信息的無線采集,最大程度上解決了一般測試方法布線繁雜等問題;而激光位移傳感器將主軸軸向的熱變形數據通過專用的控制器傳輸給上位機。
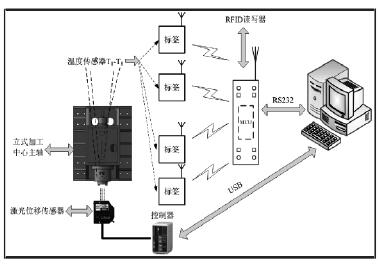
圖 2 測試系統示意圖

圖 3 現場測試圖
實驗時,設定立式加工中心主軸轉速為 3500r/min,運轉120min,并通過自編 LabVIEW 軟件對溫度傳感器及激光位移傳感器同步發送命令。采樣間隔為 3min,并對采集的各測點溫度數據和軸向熱變形數據實時顯示、存儲。實驗現場測試圖,如圖 3所示。
3.2 測點優化結果
將采集得的 8 個測點的溫度數據與主軸軸向的熱變形數據,首先輸入到 K-means 算法(初始聚類)LabVIEW 求解程序當中,設定初始聚類中心個數為 2 個,分別為第 1 列和第 3 列溫度數據,初始聚類結果,如圖 4 所示。
由初始聚類程序計算結果得,第(1、5、6、7)列溫度數據分為一類,第(0、2、3、4)列溫度數據分為另一類,并根據初始聚類的結果,求出更新中心點 0 和更新中心點 1。
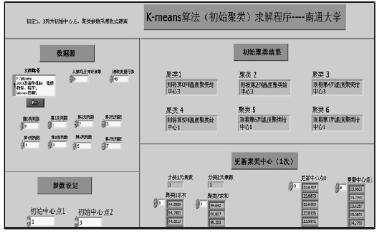
圖 4 K-means 算法(初始聚類)
再將更新中心點 0、1 和 8 個測點的溫度數據輸入到 K-means 算法(修正聚類)LabVIEW 求解程序當中,如圖 5 所示,經過多次修正,求解出最終的更新聚類中心 0’、1’,最終聚類結果為第(1、3、5、6、7)列溫度數據分為一類,第(0、2、4)列溫度數據分為另一類。
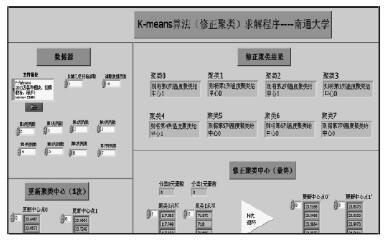
圖 5 K-均值算法(修正聚類)
最后,由于選擇的初始聚類中心對于最終聚類結果有著很大的影響,且為了達到較好的聚類效果,需要選擇不同的初始聚類中心,分別輸入 K-means 算法求解程序中,比較其誤差平方和,得出最優分類結果。結果,如表 2 所示。
表 2 溫度測點聚類分析結果
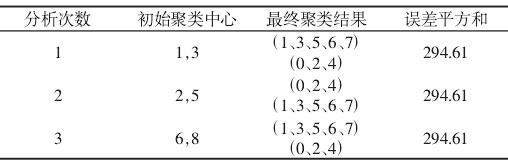
由上述結果可以看出,由三組初始聚類中心進行聚類分析的最終結果相同,則以此聚類結果作為最佳聚類結果。再利用 Pearson 相關系數計算各溫度測點數據與熱變形數據之間的相關性,從每一類中選出對熱變形影響最大的一個點。
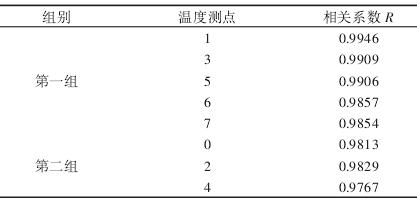
求解結果,如表 3 所示。第一類(1、3、5、6、7)中 1 號測點與熱變形之間的相關性最大,第二類(0、2、4)中 2 號測點與熱變形之間的相關性最大,由此可知,經優化后的最佳溫度測點組合為
(1,2)。
表 3 溫度測點相關性求解結果
4 、回歸建模及分析
將最佳溫度測點組合(1,2)的溫度數據和軸向熱變形數據輸入到熱誤差建模程序中求解,并通過方差分析和 F 檢驗法對模型預測能力進行評價。設溫度值 x1、x2與熱變形值 y 之間滿足如下函數關系:y=a+bx1+cx2(3)式中:x1、x2—測點 1、2 的溫度數據;y—軸向熱變形數據;a、b、c—回歸系數。
若將溫度數據 x1和 x2代入式(3)即可得到相對的熱變形值y。利用最小二乘法,建立誤差方程并轉化為正規方程,最終矩陣化求解。為避免繁雜的計算過程,利用 LabVIEW 圖形化軟件開發
界面友好的熱誤差模型求解程序,結果,如圖 6 所示。由圖 6 可以看出,所得的熱誤差模型為 y=0.00061x1+0.00136x2-0.01055,且在給定顯著水平 0.01 下,回歸方程 F> F0.01(2,40)=5.18,即在最佳溫度測點處監測的溫度與熱變形有顯著的線性關系,該回歸方程可較好地反映出熱變形的客觀變化規律。
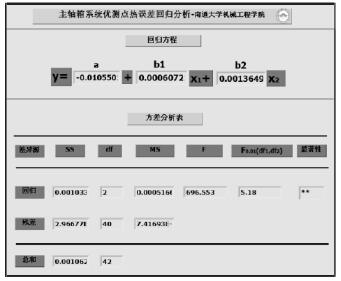
圖 6 回歸模型及 F 檢驗結果
5、 結論
(1)合理簡化主軸及箱體結構,導入 ANSYS Workbench 進行穩態熱分析,得出熱敏分析圖,利用主軸實際尺寸確定熱敏區域范圍為[88mm,265mm]。
(2)采用 K-means 算法對熱敏區域測點的溫度特征聚類,再通過 Pearson 相關系數選出與熱變形相關性最大的測點,有效地將熱敏區域內監測主軸及箱體溫度的 8 個溫度測點減少到 2 個,極大地降低了熱誤差建模的時間和成本。
(3)對優化后的溫度測點和熱變形進行熱誤差建模,并利用方差分析和 F 檢驗驗證,該模型可較好地反映出熱變形的客觀變化規律。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息





