數控車床綜合熱誤差建模及工程應用
2018-1-26 來源: 機械制造系統(tǒng)國家實驗室 河北工程大學 作者:孫志超 侯瑞生 陶濤 楊軍 梅雪松 王新
摘 要: 針對車床實際工程應用中主軸與進給軸綜合誤差對工件加工精度產生影響問題,建立包含工件膨脹效應的主軸與進給軸綜合熱誤差模型,并進行實際切削驗證. 以精密車床為研究對象,綜合分析車床主軸、進給軸和工件在實際加工中的相互影響關系,并建立三者之間的綜合熱誤差多元線性回歸模型(MLRA). 實驗結果表明:含有工件膨脹效應系數的綜合熱誤差模型符合實際工況,有效提高了車床的加工精度. 主軸熱誤差模型的預測精度達85%以上,進給軸預測精度達70%以上,實際加工中工件誤差由15 μm 降低到5 μm 左右. 綜合熱誤差模型顯著提高了高精密數控車床的加工精度.
關鍵詞: 數控車床;主軸;進給軸;工件膨脹效應;熱誤差建模;熱誤差補償
車床在軸類及盤類零件加工中占有顯要位置,我國數控車床主要存在精度低、精度保持性差等問題,影響機床精度的關鍵因素之一熱誤差占據機床總體誤差的40% ~70%[1] ,而對于高精密數控車床來說所占比重更大. 近年來,國內外針對機床熱特性的研究不勝枚舉,也取得了一些良好的效果. 楊軍等[2-5] 利用模糊聚類選擇溫度變量,建立了機床主軸熱誤差的BP 神經網絡模型、多元線性回歸模型、最小二乘支持向量機模型及時間序列模型,并在多種工況下驗證模型的準確性及魯棒性;還有學者通過實驗反求熱流密度和熱輻射等邊界條件,提高機床熱變形的仿真精度[6-8] ;Bossmanns 等[9-10] 利用有限差分模型分析并預測了電主軸熱源的分布機理;Aguado[11] 提出機床空間誤差的測量方法;Heisel等[12] 研究絲杠溫度場分布,并建立了進給軸熱誤差模型;Guo 和Shen 等[13-14] 利用不同的算法對BP 神經網絡模型進行了優(yōu)化,提高了模型精度;徑向基函數RBF(Radius Basis Function)的神經網絡模型被廣泛用于機床熱誤差建模中[15-16] ;Chen 等[17-19] 建立了主軸系統(tǒng)的多元線性回歸模型.
現有文獻都是針對主軸或進給軸單個系統(tǒng)分別建立模型,而且都是在理論上驗證模型的準確性和魯棒性,沒有進行過實際的加工驗證,實際加工中主軸與進給軸相互依賴共同影響工件的加工精度. 本文針對HTC550/500 車床建立主軸與進給軸的綜合熱誤差模型,并進行補償應用,并用實際加工來驗證模型的準確性.
1、 Siemens 系統(tǒng)熱誤差補償方式及熱特性實驗
1.1 Siemens 系統(tǒng)熱誤差補償方式
Siemens 開放了熱誤差補償接口,一定溫度下所開放的補償模型為線性模型,主軸的熱誤差只與溫度相關,與坐標位置無關;進給軸熱誤差不僅與溫度相關,且與坐標位置相關. 熱誤差模型原理圖如圖1所示.
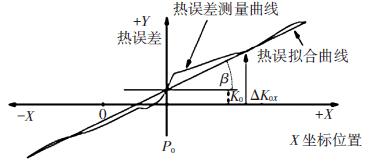
圖1 熱誤差補償原理:溫度θ 下熱誤差的近似擬合線
Siemens 內部模型:

1.2 熱特性實驗
1.2.1 實驗原理及方法
以精密數控車床為研究對象,測試設備包括:RENISHAW 激光干涉儀測量進給軸誤差;自主設計的溫度與位移同步采集系統(tǒng)測得溫度及變形數據;傳感器選用高精密溫度傳感器PT100 和高精密電渦流傳感器. 采用五點法測量主軸空間變形[ 20] ,原理如圖2 所示.
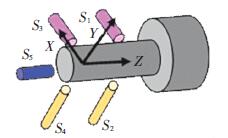
圖2 主軸熱誤差測量原理示意圖
S1、S3 為測量主軸X 方向的熱誤差, S2、S4 為測量主軸Y 向的熱誤差, S5 測量主軸Z 向的熱誤差;文獻4 中詳細介紹了利用激光干涉儀測量進給軸熱誤差的測量方法及注意事項,冷態(tài)下第一次測量進給軸誤差為機床進給系統(tǒng)幾何誤差,進給系統(tǒng)連續(xù)往復運行20 min 后測量誤差值,此誤差值減去幾何誤差作為此時進給系統(tǒng)熱誤差[4] .
1.2.2 熱特性分析
進給軸電機、軸承、絲杠螺母副等摩擦生熱導致絲杠溫度升高,絲杠向自由端方向發(fā)生熱膨脹引起絲杠導程變化. 絲杠導程變化導致半閉環(huán)控制系統(tǒng)產生誤差,進給軸的熱誤差變化如圖3 所示. 冷態(tài)下第1 次測量值為機床的幾何誤差,故冷態(tài)下機床的熱誤差為0 μm. 由圖3 可以看出,進給軸熱誤差不僅與溫度相關,而且與坐標位置相關,隨坐標值的增大而增大;負向熱誤差變化相對較小,正向熱誤差變化相對較大,由此判斷正向為進給軸自由端,即絲杠熱膨脹的方向.
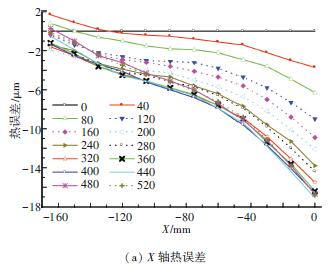

圖3 進給軸熱誤差曲線
主軸內部結構如圖4(a)所示,軸承摩擦生熱,引起主軸及外殼溫度升高,導致主軸發(fā)生熱伸長Δz和熱升高Δh. 主軸熱變形曲線如圖4(b)所示,主軸Z 向熱誤差Δz 最高達44 μm, X 向熱誤差Δx 最高達14 μm,隨著溫度的升高,主軸的熱變形隨之增大,停機后隨著溫度的降低主軸的熱變形隨之減小.
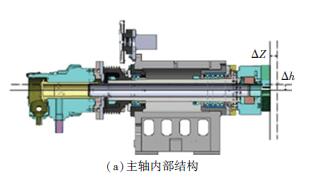

圖4 主軸結構示意圖及主軸X / Z 向熱誤差
機床熱特性實驗主軸及進給軸溫度變化見圖5.


圖5 主軸與進給軸溫度場變化
主軸傳感器PT100 配置前端3 個、中部2 個、后端3 個,前端最高溫度達35.9 ℃、后端33.8 ℃、中部32.8 ℃,其中前部最高溫差13.2 ℃、后端12.1 ℃、中部10.8 ℃. 主軸內部結構如圖4(a)所示,循環(huán)空氣冷卻中空式結構,前端3 個軸承后端1 個,導致前端發(fā)熱量最大,后端次之,中部最小,溫度場變化與結構相符合. 由圖5(a)和圖4(b)對比可看出,曲線變化規(guī)律一致,變形與溫度之間具有一定的線性關系.
進給軸傳感器PT100 配置主要在電機、軸承及絲杠螺母座上,通過螺母座溫度間接反映絲杠溫度變化. 其中,電機溫度變化最大,床身溫度變化最小;前軸承溫度大于后軸承; Z 軸螺母座溫度大于X軸螺母座.
2、熱誤差建模及補償實現
2.1 綜合熱誤差建模

在車床加工過程中,主軸與進給軸熱誤差相互耦合共同影響工件的精度,因此需要建立主軸與進給軸的綜合熱誤差模型.
2.1.1 主軸熱誤差模型
主軸熱特性實驗中,電渦流傳感器的安裝位置影響測量結果,以X 向熱誤差測量為例說明. 圖6 為主軸熱特性實驗傳感器安裝主軸軸向視圖

圖6 傳感器安裝主軸軸向示意圖
傳感器的安裝支架安裝在刀塔上. 實驗過程非恒溫,環(huán)境溫度的升高導致絲杠溫度升高,并伴隨著熱伸長, X 軸絲杠熱伸長導致刀塔位置發(fā)生變化,從而引起傳感器相對于測量芯棒的位置變化,導致傳感器測量主軸X 向熱誤差就包含了X 軸絲杠熱變形誤差. 因此,主軸X 向熱誤差建模中要消除X 軸絲杠的熱變形誤差,處理方法:
2.1.2 進給軸熱誤差模型
由于軸承及絲杠螺母副摩擦發(fā)熱,絲杠溫度升高導致進給系統(tǒng)產生熱誤差. 然而,在實際加工中工件也會發(fā)生熱脹冷縮現象,同樣會影響工件的加工精度. 圖7 為工件與絲杠變形示意圖. 相同溫度下所有工件的長度均為L, 在相同溫升條件下工件1、2、3 的膨脹量分別為Δ1、Δ2、Δ3, 絲杠在相同長度L 上的膨脹量為ΔS. 當工件的膨脹系數<絲杠的膨脹系數,即當ΔS > Δ1 時,絲杠的膨脹量大于工件的膨脹量,此時的補償量為絲杠與工件膨脹量的差值,方向為絲杠膨脹反方向;當絲杠的膨脹系數等于工件的膨脹系數,即當ΔS = Δ2 時,絲杠的膨脹量與工件膨脹量相同,此時絲杠的膨脹量剛好補償了工件的膨脹量,不需要對絲杠的膨脹量進行補償;當絲杠的膨脹系數小于工件的膨脹系數,即ΔS < Δ3 時,絲杠的膨脹量小于工件的膨脹量,此時的補償量亦為絲杠與工件膨脹量的差值,方向為絲杠膨脹方向.因此,進給軸的熱誤差補償要考慮工件的膨脹效應,補償方法:


圖7 工件與絲杠變形示意圖
2.1.3 綜合熱誤差模型
選取主軸及床身溫度為溫度變量,結合MLRA方法得到如下主軸的熱誤差模型:
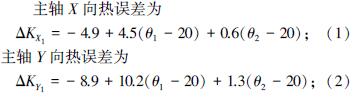

式中: θ1、θ2、θ3、θ4 分別為床身、主軸、X 軸螺母和Z軸螺母溫度; tan β (θ)speed-X 、tan β (θ)speed-Y 分別為
X、Y 軸絲杠膨脹系數; PX 、PY 為進給軸坐標; P0X 、P0Y 為進給軸參考點坐標值. 模型中將20 ℃作為參考溫度是因為GB 中將20 ℃ 作為檢測時標準環(huán)境溫度,機床定位精度檢測標準環(huán)境溫度亦為20 ℃.
圖8、9 為主軸及X / Z 進給軸熱誤差模型預測值與實驗值的對比圖. 建立模型預測精度評價標準均方根誤差值RMSE 及預測精度η[5] . 其中R 為均方根誤差值, yi 為實驗測量值, y~i 為模型預測值. 主軸X / Z 方向熱誤差模型的R 和η 分別為2. 5、5.2 μm和89.4%、88.7%; X / Z 進給軸熱誤差模型的R 和η 分別為2.4、5.1 μm和84.5%、82.7%. 說明熱誤差模型有一定準確性,應用效果還需進一步驗證.
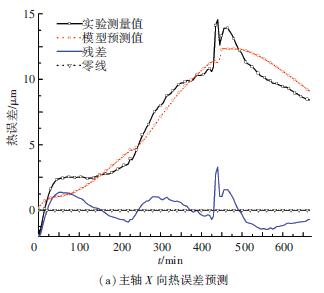
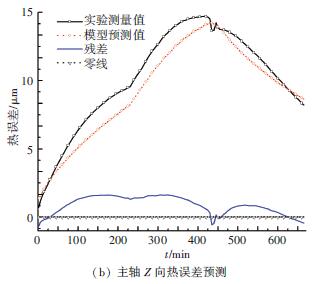
圖8 主軸熱誤差模型預測值與測量值的比較


圖9 進給軸熱誤差模型預測值與測量值的比較
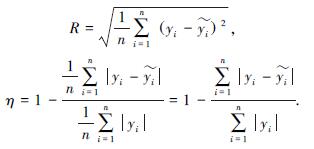
機床主軸系統(tǒng)與進給軸系統(tǒng)為相對獨立的個體,實際加工中二者缺一不可,軸與進給軸的熱誤差相互關聯共同影響工件的加工精度. 得到主軸與進給軸熱誤差的相互關系對于模型的建立尤為重要.主軸系統(tǒng)由于軸承及加工摩擦生熱造成主軸系統(tǒng)溫度升高,隨之產生熱變形Δlz 、Δh, 絲杠受熱發(fā)生膨脹導致進給系統(tǒng)產生熱誤差Δx、Δz, 如圖10 所示.由于X 軸是傾斜式安裝,主軸熱變形Δh 在機床X方向產生分量Δlx , 方向與X 進給軸相同;主軸熱伸長Δlz 方向與Z 進給軸方向相同. 因此機床X / Z 方向的熱誤差模型應該是主軸與進給軸的綜合熱誤差模型. 結合式(1) ~(4)及文章2.2.1、2.2.2 節(jié)分析得到機床在X / Z 方向的綜合熱誤差模型.

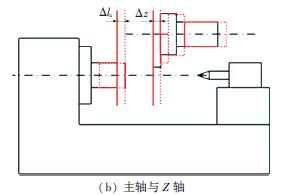
圖10 主軸與進給軸熱誤差耦合示意圖
X 方向熱誤差模型:
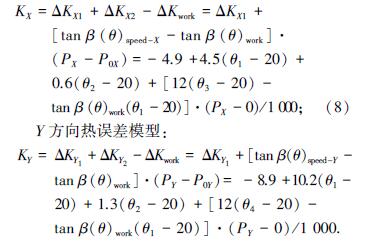
2.2 補償實現及實際加工分析
2.2.1 補償實現
Siemens828D 熱誤差補償總體方案如圖11 所示,由PLC 直接獲取機床熱源溫度值,在PLC 內計算補償參數,最后PLC 通過數據接口DB1200 將補償參數寫入NC 系統(tǒng)內,系統(tǒng)根據補償參數及插補指令計算正確的電機指令從而達到補償效果,提高機床的加工精度.
冷態(tài)下測量機床的定位精度,隨后同時運轉主軸及進給軸系統(tǒng),模擬實際加工主軸與進給軸熱誤差耦合現象,驗證綜合熱誤差模型的準確性,直到機床達到熱平衡狀態(tài). 測量機床熱誤差補償前后的定位精度,結果如圖12 所示. 熱補償前X / Z 軸定位精度分別為19.8 μm、27.2 μm;熱補償后X / Z 軸定位精度分別為6.9、9.1 μm,熱補償后X / Z 軸定位精度分別提高了65.2%、68.4%,表明熱誤差綜合模型有一定的補償效果.
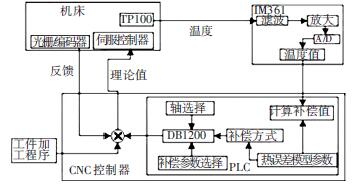
圖11 Siemens828D 熱誤差補償總體方案

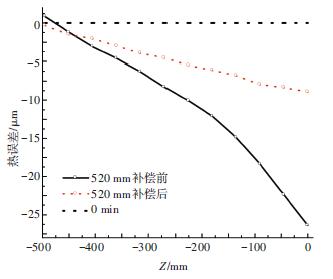
圖12 X / Z 軸熱平衡下熱誤差補償前后對比
2.2.2 實際加工分析
加工工件如圖13 所示,嚴格按照工程實際在有無熱誤差補償狀態(tài)下按圖紙要求進行加工,兩種狀態(tài)下各加工一天,對工件按照加工順序做編號. 將加工好的工件置于20 ℃的恒溫環(huán)境中8 h 以上,按編號使用三坐標測量儀測量工件R1、R2 的直徑,記錄于表格,比較有無熱誤差補償狀態(tài)下的工件誤差。
實際結果如圖14 所示. 由圖14 可知,在有無熱誤差補償狀況下工件誤差首先負向變大而后向正向變化,這是由于X 軸絲杠的安裝在X 負向有預拉伸,絲杠溫升初始時首先要消耗預拉伸量,因此導致工件誤差負向變化. 圖14(a)所示預拉伸消耗之后工件誤差正向有明顯變化,跨度15 μm,這便是熱誤差造成的影響;圖14(b)所示預拉伸消耗之后工件誤差有了明顯改善,跨度5 μm 左右,由此證明熱誤差補償的準確性.

圖13 加工工件

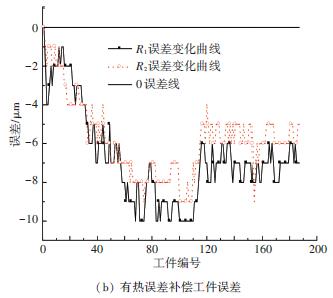
圖14 有無熱誤差補償時的工件誤差
3、 結 論
1)本文研究了Siemens828D 系統(tǒng)的熱誤差補償機制,分析了主軸與進給軸熱誤差之間的相互關系,建立了綜合熱誤差模型,并考慮了工件的膨脹效應對模型的影響.
2)利用PLC 與NC 之間的數據接口DB1200 實現了補償數據的通信,加工過程中監(jiān)測溫度并進行實時補償.
3)并進行了切削加工試驗,有效驗證了熱誤差的補償效果.
投稿箱:
如果您有機床行業(yè)、企業(yè)相關新聞稿件發(fā)表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業(yè)、企業(yè)相關新聞稿件發(fā)表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息





