基于剛體動力學的五軸數控機床模擬系統研究
2016-8-1 來源:天津職業技術師范大學 作者:岳剛
把操作者手工編寫或通過軟件自動編寫的工件加工程序,翻譯成運動控制卡可以識別的刀具路徑軌跡,是數控系統的主要工作之一。這個識別過程實際上是將工件加工程序中工件坐標系中的刀具路徑軌跡經過一定的計算[20],轉變成為機床坐標系中的刀具路徑軌跡。所以必須正確的對刀具路徑軌跡進行運動求解計算才能實現該過程。五軸數控機床通過在三個線性軸運動的基礎之上增加了兩個回轉軸的運動[21],其運動的復雜性也相應的增加,對于編程人員和機床操作人員來講,增加了一定的難度。對五軸數控機床進行正確的運動求解,有利于深入掌握它的運動規律,最大程度地發揮其在加工中高效、高精等優勢。
從數學的角度講,物體運動求解的本質就是三維圖形的線性變換,其中包括基礎線性變換,諸如平移變換、旋轉變換等。當前國內外相關行業的研發人員已開始對適合五軸數控機床進行分析的通用算法的探究,不過目前針對五軸數控機床的運動分析大多是在假定機床所有移動軸一一正交等限制條件下進行的[22],并且也沒有考慮機床本身的制造精度。所以,綜合考慮多因子的五軸數控機床運動分析理論的探究是今后五軸數控機床運動學探究最主要的領域之一。
本章在描述了運動分析時所必須借助的基礎線性代數原理,分別例舉了采用三種非常普遍的構成形式的五軸數控機床在一定的限制條件下的運動分析算法。因為機床的制造精度與安裝精度有一定限制,故對于五軸數控機床進行運動分析還需要結合機床自身具有的許多誤差,來修正這些誤差對工件切削精度的影響。
3.1 運動分析
在三維空間中,任何物體的運動方式都可以概括為幾何體的平移、旋轉等許多基礎的線性變換[23]。從線性代數的角度講,這些變換全部可以看做幾何體的幾何變換,因此又把幾何體的線性變換稱為幾何變換,上述的變換能夠通過線性代數中的矩陣乘法來完成。
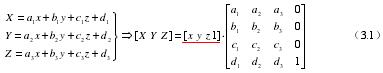
3.1.1 平移變換
幾何體在三維空間從一個坐標點沿著任意直線運動到另一個坐標點的過程叫做平移變換[23],在整個變換中不會使幾何體的外形和尺寸發生變化。對應的齊次方程為:

假定空間幾何體的起始位置為(x,y,z),在整個運動過程中,幾何體沿著 X、Y、Z 三個方向各運動了 u、v、w 個單位長度,運動結束后,新的位置為(X、Y、Z),那么該幾何體的位置變換對應的方程為:

3.1.2 旋轉變換
所謂旋轉變換,就是讓某個物體繞著 X、Y、Z 三個軸中的一個軸旋轉一個角度。此時,可以利用右手螺旋法則來判斷轉角的正負[24][36]。(1)圍繞 X 軸轉動,X 方向坐標不發生變化,只有 Y、Z 兩個方向坐標發生變化。對應的方程為:
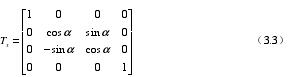
(2)圍繞 Y 軸轉動,Y 方向坐標不發生變化,只有 Z、X 兩個方向坐標發生變化。對應的方程為:
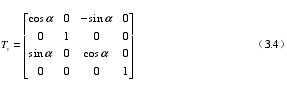
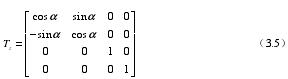
(3)圍繞 Z 軸轉動,Z 方向坐標不發生變化,只有 X、Y 兩個方向坐標發生變化。對應的方程為:
3.1.2.1 圍繞過(0,0)點的任意直線的旋轉變換
直線 OD 是給定三維坐標系中過(0,0)點的任意直線,點 F 是坐標系中任一不在直線OD 上的點,若點 F 圍繞直線 OD 轉動后與 G 點重合,那么相應旋轉變換的計算方法為[25]:
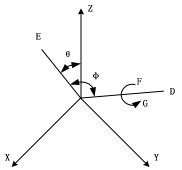
圖3-1 繞過坐標原點直線的旋轉
(1)令直線 OD圍繞 X 軸轉動轉角后與面 XOZ 重合,新的直線成為 OE。這個變換能夠用式 3-3 來完成。
(2)令直線 OE 圍繞 Y 軸轉動轉角 θ 后與 z軸重合,這個變換能夠用式 3-4 來完成。
(3)使用式 3-5 令點 P 圍繞 Z 軸轉動轉角 α。
(4)運算和(2)中互逆,也就是令直線 OE 圍繞 Y 軸旋轉轉角-θ,即使用式 3-4 的互逆矩陣來完成。
(5)運算和(1)中互逆,即使用式 3-3 的互逆矩陣來完成。最后能夠獲得圍繞過(0,0)點的任意直線 OD 的旋轉矩陣1 1R x y z y xT T T T T T= 。
3.1.2.2 圍繞過其他已知點的任一直線的旋轉變換
L 是三維空間中過點的任一直線,它的方向向量是,那么空間幾何體圍繞直線 L 轉動轉角的相應轉換能夠分為如下三步:
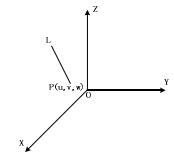
圖 3-2 繞過任意點 P 直線的旋轉變換
(1)通過空間幾何體與直線 L 共同進行平移令點 P 移動到(0,0)點位置,轉換矩陣pT為:
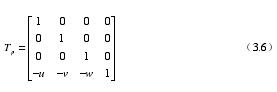
(2)在前一個步驟完成之后,令空間幾何體圍繞 L 轉動轉角α ,對應轉換矩陣是RT 。
(3)令空間幾何體與 L 共同進行平移變換回到最初坐標,對應轉換矩陣是1PT:

最后,能夠獲得總的轉換矩陣:
3.2 常見五軸數控機床的構造模式
從三維幾何的角度講,每一個物體都擁有六個獨立的自由度[27]。舉個例子,對于一個工件來說,工件的位置是固定的,所以,對于工件來說,主軸就具備了六個獨立的自由度。在加工過程中,主軸上的刀具對工件進行切削,這時刀具軸線也就是主軸軸線和工件之間的距離受到刀具半徑的限制,因而實際上只有五個自由度可用,理論上講實現五軸聯動就可以完成所有空間復雜曲面的加工[28]。
五軸數控機床通常指擁有五個以上可聯動軸的數控機床[29],依據不同的自由度組合方式也就是固定或變相固定哪一個的自由度,理論上能夠形成成四種不同的組合,依次為:X、Y、Z 三個軸方向上的自由度和繞任意兩個軸回轉的自由度組合、任意兩個直線方向自由度和三個回轉自由度組合、一個直線方向自由度和四個回轉自由度組合、五個回轉自由度。但在實際使用過程中,需要考慮機床的綜合性能,特別是加工精度、系統壽命等關鍵要素,所以,當前市場上常見的五軸數控機床都普遍采用第一種方式的自由度組合[30]。依據不同的回轉自由度,還能夠對五軸聯動數控機床進行細分,可以分為三種,分別是:雙旋轉主軸頭式、雙回轉工作臺式、一回轉工作臺加一旋轉主軸頭式[31]。
(1)雙旋轉主軸頭式
雙旋轉主軸頭式的五軸聯動數控機床示意圖如圖 3-1 所示。從圖中能夠發現,機床的兩個回轉自由度全部布置在主軸上,使得刀具能夠前后左右進行擺動,這樣理論上可以使刀具繞中心點轉動到任意位姿[32],對于此類機床,其工作臺無需進行轉動,因此工作臺的大小不受約束,允許設計者設計大型機床。這樣的布置形式的特點在于機床整體承載性能大大增強[33],同時加工空間也基本不受限制,其加工對象為大型工件,所以大型龍門式五軸聯動數控機床普遍的采用這種結構。此類機床兩個旋轉軸全部集中到了刀具的上部,回轉軸部分結構緊湊,加工過程靈活;同時缺點也很明顯,因為主軸頭集成的擺動機構與傳動機構過于復雜,使得整個機床的剛度被大大降低。
(2)一回轉工作臺加一旋轉主軸頭式
這種類型的機床通過在機床的主軸頭上面加一個回轉自由度,另外一個回轉自由度加在工作臺上,主要通過加載在主軸和工作臺上的兩個方向的回轉自由度,這樣布置的好處就是兩個回轉軸的軸線方向都是固定不變的[33],其示意圖如圖3-2 所示。這種結構的五軸機床,因為兩個方向的回轉運動并未集中在一起,所以采用這類布置方式的五軸數控機床優點是結構簡單、整體剛性好,缺點是靈活性不好。由于只有一個回轉自由度在工作臺上,導致整個機床的承載性能差,并且只能承擔的尺寸相對較小的加工任務,通常用來進行中等尺寸工件的切削。

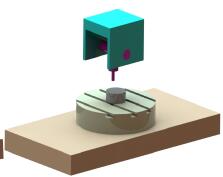
圖3 -1雙旋轉主軸頭結構五軸機床 圖3 - 2一擺動頭和一回轉臺結構五軸機床
(3)雙回轉工作臺式
這種類型的五軸聯動數控機床(圖3-3)是由工作臺承擔兩個回轉自由度的,因為主軸和工作臺的運動是相對的,所以不論旋轉自由度布置在主軸上還是布置在工作臺上,都能達到同樣的加工效果從傳動鏈的先后順序能夠知道,采用這種布置方式的機床的兩個旋轉軸有一個是定軸另一個是動軸。定軸就是指遠離工件的只具備一個旋轉自由度的軸[34],這個軸圍繞的軸線方向在加工過程中是不會改變的;動軸是指跟著加工工件一同擺動的旋轉軸,其所圍繞的旋轉軸線方向跟著一個定軸的運動而旋轉。采用這種布置方式的機床承載性能最差,加工尺寸范圍最小,整個系統剛性處于中等水平,通常用于中小尺寸工件的切削加工[35]。
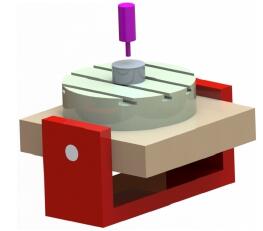
圖3-3雙回轉工作臺結構五軸機床
綜上所述,無論五軸機床采用哪種布置方式,都同樣可以做到刀具對工件的任意角度切削。因為機床擁有兩個旋轉自由度,刀具可以在機床結構的限制下的任意空間角度對工件進行切削。在相應運動控制算法的支持下,能夠確保在整個切削過程中,刀具按照最佳的位姿來加工,而且可以防止機床發生運動干涉[36]。所以,五軸聯動數控機床具備三軸、四軸機床所不具備的的優越的性能,能完成分任務更多,同時精度會更高[37]。
重點研發五軸數控機床模擬訓練機的意義在于:學習數控系統最好的方式是在實際機床上進行練習,但是這樣需要大量的五軸數控機床,這對于學校來說是不現實的[38]。五軸數控機床模擬訓練機是國內首創能夠解決數控系統教學問題、數控編程人員學習問題的一個關鍵產品。
3.3 五軸數控機床的運動求解
3.3.1 雙轉臺型五軸數控機床的運動求解
雙回轉臺型五軸數控機床按照旋轉軸的不同,能夠具體分為 AB、BC、AC 三種[39]。因為這三種不同選擇方式的運動變換計算過程沒有太大差別,所以在這里只探討了最常見的 AC 型組合方式的運動變換計算過程[40]。
傳統三軸數控機床只具備 X、Y、Z 三個直線方向的自由度[41],所以沒有必要進行其他的分析、數學建模、運算,只需要將程序中的有關路徑控制方面的 G 代碼翻譯成 XY、Z 三個軸方向上的運動量,然后再進行聯合插補運動,最終就能夠驅動三個運動軸切削工件。五軸數控機床除了擁有 X、Y、Z 三個軸之外還有另外兩個回轉軸[42],使得刀具可以相對于工件做直線移動和回轉運動,所以在刀路運動計算上,需要六個數據來表達某一瞬時的刀尖點位置及刀具軸線位姿:(X, y , z )表示加工刀尖點的位置,( i , j , k )表示加工刀具軸線的位姿[43]。
在五軸機床中,刀具在對工件進行切削之前,需要嚴格采用五軸機床上的結構形式對其整個運動、切削過程進行運動學分析,找出工件坐標系與機床坐標系的聯系,推算出其中的轉換矩陣,充分利用這個轉換矩陣[44],能夠精確的轉換某一瞬時的刀尖點位置及刀具軸線位姿為 X、Y、Z 三個軸的移動和 A 、C 兩個旋轉軸的轉動,這一點是保證數控程序能夠正確被編譯的基礎。本節會針對此推導過程做詳細討論[45]。
如圖 3-4 所示,記工件原點坐標系為m m m0X Y Z ,機床原點坐標系為t t tO X Y Z ,以 A、C兩軸中心線交點作為機床坐標原點[46]。工件原點坐標系m m mO X Y Z 和機床原點坐標系t t tO X Y Z 共享同一個 Z 軸方向,m t0 O =d 。工作臺的回轉能夠帶動毛坯進行位姿變換,其中 A、C 兩軸的轉動范圍分別為 0°≤A≤90°、0°≤C≤3600°。
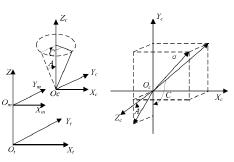
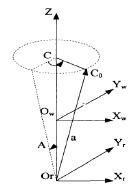
圖 3-4 坐標系 圖3 - 5雙轉臺型五軸數控機床坐標系
為了方便以后的計算,需要定義一下計算過程中用到的坐標系:令零件坐標系為w w w wO X Y Z ,零件能夠在兩個回轉軸的運動中完成圍繞 X 軸轉動轉角 A( 0° ≤A ≤90° ),圍繞 Z 軸轉動轉角 C;機床的移動坐標系為r r r rO X Y Z 。同時,w rO O =d ,如圖 3-5 所示;當前刀具的刀心點0C ,其在零件坐標系內的坐標假定為(0 0 0, ,C C CX Y Z );當前刀具的軸線假定為α (單位矢量),其在零件坐標系內假定為( , ,)x y zα α α[48]。
在以上設定的基礎上,AC 型組合方式的運動變換計算過程具體如下:
(1)首先將刀具軸線α 移動到經過零件坐標系的原點,之后令它圍繞 Z 軸轉動到平面(-Y)(+Z)內,最后把刀具軸線α 圍繞 X 軸轉動到和 Z 軸重合[49]。以上工作的出發點是要確保當 0zα ≥ 時,令刀具軸線 α 圍繞 X 軸轉動轉角處于 (90° 0°) 之間,也就是刀具相對于零件圍繞 X 軸轉動轉角處于(0° 90°) 之間。
(2)將刀具軸線α 的轉動轉化成刀具的旋轉或移動:首先讓刀具圍繞 X 軸轉動某個角度 A,再將刀具圍繞五軸機床德爾 Z 軸轉動一定角度 C。所以能夠獲得 A 角的運算過程如下:
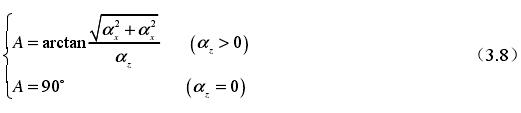
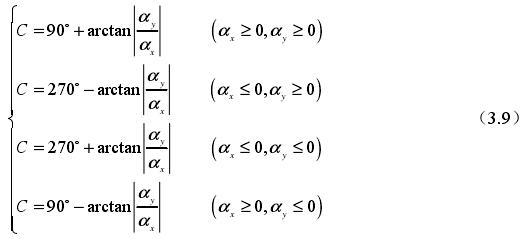

(3)零件坐標改變后,刀具的中心點0C 坐標值也會發生變化,則機床坐標系內的坐標值 X、Y、Z 的運算方法為:
1)對零件工件坐標系w w w wO X Y Z 進行移動,使得兩個坐標系的rO 和wO 重合,相應的轉換矩陣是:

2)使零件圍繞五軸數控機床的 Z 軸轉動角度 C,對應的轉換矩陣是:
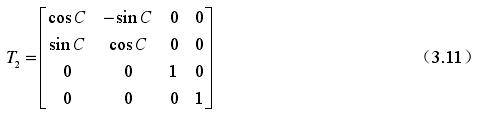
3)使零件圍繞五軸數控機床的 X 軸轉動一個角度 A,相應轉換矩陣是:

則有:
將上式展開可得:
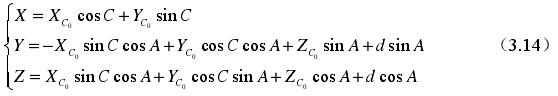
3.3.2 雙擺頭型五軸數控機床的運動求解
雙擺頭型五軸數控機床根據不同的旋轉軸,可以細分為三種方式[50]。因為這三種不同選擇方式的運動變換計算過程沒有太大差別,所以在這里只探討了最常見的 X,Y,Z,A,C 組合方式的運動變換計算過程[51]。
首先,初定零件坐標系為w w w wO X Y Z ,假定讓刀具繞 Z 軸旋轉一定角度 C,再讓刀具圍繞 X 軸旋轉一定角度 A(0 ≤A ≤90);假定刀具的轉動中心0hC 至刀心點0C 的空間上的直線距離是 L,如圖 3-6 所示。此時,刀心點0C 處在零件坐標系內的位置為0 0 0(, , )C C CX Y Z ,同時,刀具軸線α (單位矢量)在零件坐標系內可用( , , )x y zα α α 來表示。那么,機床坐標系內移動變換可以表示為:
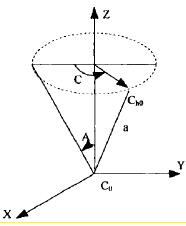
圖 3-6 雙擺頭型五軸數控機床坐標系
A、C 角的計算過程和前一節里的計算過程并無差別,在這里就省略了。
刀具中心0hC 在刀具旋轉和移動后位于零件坐標系w w w wO X Y Z 內的坐標,就是機床坐標系下 X,Y,Z 坐標值,其計算過程為:
(1)如圖所示,刀具中心以刀心點0hC 為固定點轉動轉角0C ,圍繞 X 軸轉動轉角 A,它的轉換矩陣是:
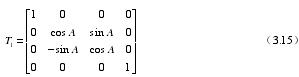
(2)刀具中心以刀心點0hC 為固定點轉動轉角0C ,圍繞 Y 軸旋轉轉角 C,它的轉換矩陣是:
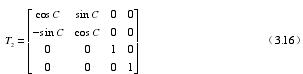
(3)經過以上轉換之后,刀具中心位于零件坐標內的位置能夠通過下面的方程來計算:
將上式展開得:
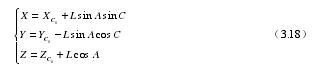
3.3.3 非正交五軸數控機床的運動求解
這種運動方式的求解與以上兩類運動變換相似,計算過程并沒有很大的差別,非正交結構五軸數控機床的運動可以具體劃分為幾下三步進行變換計算[52]:
(1)計算從零件坐標系轉換至機床坐標系的位置轉換矩陣。
(2)計算相對于起始點的兩個轉動軸的轉角。
(3)把零件坐標系內具體的刀位點位置變換成實際機床坐標系中的坐標值[53]。因為本文具體討論的是雙轉臺正交構造的五軸數控機床,并且非正交構造五軸數控機床的移動變換計算過程相對繁瑣,所以本文不討論。
3.4 本章小結
伴隨著電子計算機科技、數字控制算法的飛速進步,切削加工工件復雜程度的增加等,五軸數控機床在構造構成以及數字控制算法上均表現出多樣化的發展態勢[54]。本章首先闡述了平移、旋轉等對機床進行運動求解時必需的一些基本數學理論。接著從結構形加工性能等角度,對雙轉臺型、雙擺頭型、擺頭轉臺型以及非正交型五軸數控機床進行了詳細的介紹,并詳細了研究了上述幾種常見類型機床的運動求解算法[55]。本章在描述了運動分析時所必須借助的基礎線性代數原理,分別例舉了采用三種非常普遍的構成形式的五軸數控機床在一定的限制條件下的運動分析算法[56]。同時,為下一章的進一步研究做了鋪墊,為模擬機訓練系統操作模塊研究奠定了基礎。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多本專題新聞
專題點擊前十
| 更多










