0 引言
磨削加工是現(xiàn)代機(jī)械制造業(yè)中進(jìn)行精密加工和超精密加工的重要工藝技術(shù)。在磨削加工中,所消耗的能量大部分轉(zhuǎn)化為熱能傳入被磨工件,傳入工件的熱量主要集中在很薄的表面層里,形成局部高溫,這種現(xiàn)象對工件表面質(zhì)量和工件的使用性能影響很大。國內(nèi)外大量專家學(xué)者對磨削加工中的熱效應(yīng)問題進(jìn)行了研究。1942 年,J. C. Jaeger[1] 首先提出了移動熱源理論,Outwater 和Shaw[2] 基于剪切面移動熱源理論建立了熱量傳遞給工件的熱源模型, 1996 年Rowe[3] 在前人研究的基礎(chǔ)上綜合考慮了工件的熱特性、砂輪的鋒利程度、砂輪和工件的速度、切深以及接觸長度對溫度場的影響。我國學(xué)者貝季瑤教授[4] 早在上世紀(jì)60 年代就提出了熱源強(qiáng)度在沿接觸弧長上為三角形分布的假設(shè),高航教授[5] 在研究斷續(xù)磨削時分別建立了臥軸周邊斷續(xù)磨削和立軸端面斷續(xù)磨削的熱源模型。磨削過程的熱效應(yīng)一直是國內(nèi)外學(xué)者研究的熱點(diǎn)。
隨著航天和汽車技術(shù)的發(fā)展,出現(xiàn)了越來越多的薄片類零件,如航天倉中的各種密封圈和墊片。這類零件的磨削質(zhì)量要求很高,磨削過程中的熱效應(yīng)容易使零件變形和燒傷,影響了磨削質(zhì)量和使用性能。精密磨削過程中的熱效應(yīng)問題,已逐漸成為制約薄片類零件磨削加工工藝發(fā)展的瓶頸,因此在這種情況下對薄片零件平面磨削工藝參數(shù)優(yōu)化問題的研究具有極大理論和實(shí)際應(yīng)用價值。
1 薄片零件平面磨削表面溫度場的計(jì)算理論研究
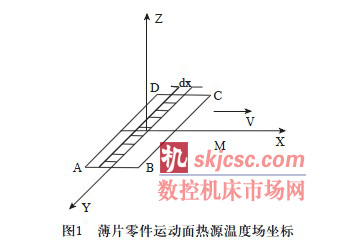
如圖1 所示面熱源ABCD 沿X 方向以速度V在無限大的薄片零件內(nèi)運(yùn)動。
按照兩維傳熱模型計(jì)算,則薄片平面內(nèi)X 軸上任意一點(diǎn) 的溫升為[6]
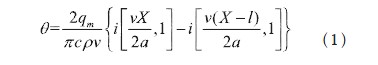
根據(jù)式(1)可以計(jì)算薄片零件表面內(nèi)沿X 軸方向上任意點(diǎn)的溫度。
按照一維傳熱模型計(jì)算,將面熱源看成只沿Z方向傳入零件內(nèi)。則當(dāng)面熱源運(yùn)動到M 點(diǎn)后,在面熱源區(qū)域下Z 方向上任意點(diǎn)的溫升為[6]。
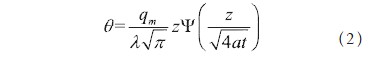
薄片零件磨削區(qū)表面的溫升為
![]()
由于移動面熱源在任一瞬間同時存在兩維傳熱和一維傳熱,如圖2 所示。設(shè)有qm 的熱量按一維傳熱,忽略其它熱量損失,根據(jù)能量守恒則有) qm 的熱量按照兩維傳熱。
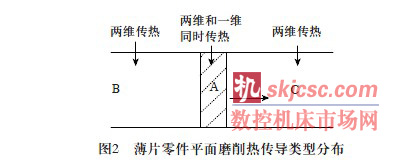
則薄片零件表面磨削區(qū)任一點(diǎn)的溫升可表示為:
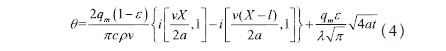
令= f (v),且0 < < 1,當(dāng)工件移動速度v →∞時, → 0 ;公式(4)等效于公式(1)兩維傳熱,當(dāng)工件移動速度v → 0 時, → 1 公式(4)等效于公式(2)按一維傳熱。對于磨削區(qū)中確定一點(diǎn),在其它磨削參數(shù)不變的情況下,某一確定時刻
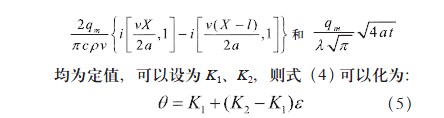
分布取不同的工件移動速度V,并測出磨削區(qū)表面在每個工件移動速度下的最高溫度,代入公式(5)令X = 0 經(jīng)查表[6] 可以求出。如表1 所示。
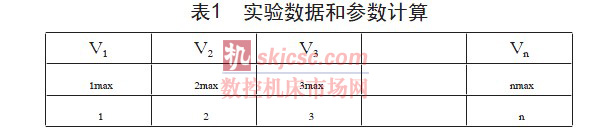
由若干組V 和,用數(shù)學(xué)插值的方法可以確定函數(shù)= f (v),又因?yàn)榘l(fā)熱功率qm = f (Ft, vs)[6],其中Ft 是切向磨削力,vs 是磨削速度。所以
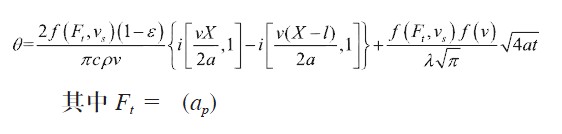
2 薄片零件平面磨削工藝優(yōu)化
平面磨削最重要的三個參數(shù)是磨削深度ap、磨削速度vs、工件的進(jìn)給速度v。薄片零件平面磨削工藝優(yōu)化的主要目的就是選擇合適的磨削參數(shù),使磨削溫度最低,即求函數(shù)值最小。這是一個數(shù)學(xué)問題。構(gòu)造拉格朗日函數(shù)
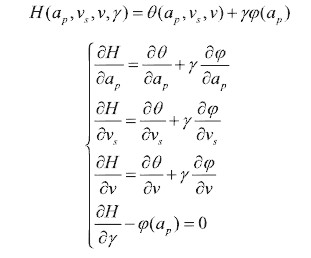
滿足該方程組的所有解(ap, vs, v) 都可能是極值點(diǎn),分別將這些解帶入溫度場函數(shù),比較大小,找出使溫度最小的那組解就是我們磨削工藝優(yōu)化的參數(shù)。
3 結(jié)論
本文用數(shù)學(xué)理論方法找到了磨削工藝參數(shù)的優(yōu)化解,該方法節(jié)省了以往依靠工人經(jīng)驗(yàn)或采用大量實(shí)驗(yàn)來優(yōu)化工藝而浪費(fèi)的人力和物力,節(jié)省了時間,提高了效率,降低了成本,具有一定的實(shí)際應(yīng)用價值。
如果您有機(jī)床行業(yè)、企業(yè)相關(guān)新聞稿件發(fā)表,或進(jìn)行資訊合作,歡迎聯(lián)系本網(wǎng)編輯部, 郵箱:skjcsc@vip.sina.com










