弧齒非圓形錐齒輪的銑削加工方法
2021-5-19 來源:- 作者:-
摘要: 弧齒非圓形錐齒輪的各個齒形參數不同,加工方法復雜。為解決其切削加工難題,基于圓錐齒輪的嚙合原理,提出了一種弧齒非圓錐齒輪的數控銑削加工方法。根據非圓錐齒輪的節曲線數據和齒輪嚙合理論,推導出加工參數及成型盤銑刀和被切輪坯的瞬時位置公式,并用 Matlab 數值法求解出一系列刀具和輪坯的位置坐標,計算結果作為數控加工程序的控制參數,可用五軸 NC 機床加工弧齒非圓錐齒輪。加工實例說明該方法正確,可以提高加工精度和加工效率。
關鍵詞: 弧齒非圓錐齒輪; 數值方法; 數控機床; 加工參數; 銑削
0 引言
圓錐齒輪在車輛差速器、機床傳動箱等傳動機械上廣泛應用。非圓形錐齒輪( 也稱球面非圓齒輪) 可以傳遞變傳動比,在不改變原有差速器結構前提下,可以實現車輛差速器的限滑功能。但由于設計與加工難度,非圓形錐齒輪的應用受到限制。求解和加工球面非圓齒輪的研究不多,尤其是加工方法,由于其結構形狀復雜,目前非圓形錐齒輪可采用線切割方法,也有采用成型鑄造方法,或者成型刀具電火花加工。
上述方法的缺點一是加工精度不高,嚴重依賴刀具精度;二是加工效率低,需要先加工非圓錐齒形毛坯然后采用電火花加工; 而且線切割方法只能加工直齒錐齒輪。近來隨著加工技術的發展,非圓形錐齒輪的應用研究逐漸增多。本文基于圓錐齒輪的嚙合原理,研究采用盤形銑刀在數控機床上加工弧齒非圓形錐齒輪的方法。不僅可以直接成型,精度高,而且弧齒非圓形錐齒輪可以提高嚙合傳動重合度,使傳動平穩。
1 、弧齒圓錐齒輪加工原理
弧齒圓錐齒輪的切齒是按照“假想平頂齒輪”的原理進行的,如圖 1 為弧齒錐齒輪的“假想齒輪”切齒原理,圖 1a 為假想平頂齒輪和刀具、輪坯位置。
在調整切齒機床的時候,必須使被切齒輪的節錐面與假想平頂齒輪的節錐面相切并做純滾動,而刀頂旋轉平面則需和被切齒輪的根錐相切,假想平頂齒輪和被切齒輪關系如圖 1b 所示。
所以銑刀盤軸線與被切齒輪的節錐面傾斜一個大小等于被切齒輪齒根角 γ 的角度。
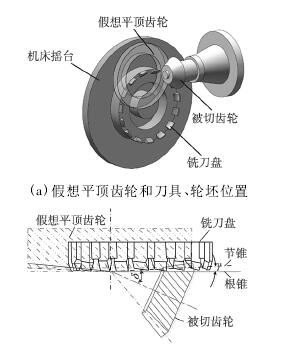
圖 1 弧齒錐齒輪的“假想齒輪”切齒原理
2、 弧齒非圓形錐齒輪數控銑削加工方法
對于圓錐齒輪,節曲線是圓,而且各個齒均一樣,加工時被切齒輪坯起始位置可為任意位置,旋轉角度也固定,四軸數控機床即可完成,4 個自由度分別是:銑刀盤的軸向移動和繞軸轉動,被切輪坯軸向移動的轉動。
而對于非圓的錐齒輪,其節曲線是球面上的特殊曲線,在每一周期內每個齒不一樣 ( 如圖 2 為一對嚙合的非圓錐齒輪節曲線,傳動比為正弦周期曲線,圖 3 為非圓直齒錐齒輪) ,且傳動時瞬時傳動比都不一樣,因此,被切輪坯的每個齒起始位置和轉動角度、轉動速度都不一樣,輪坯和刀具的瞬時位置都需要根據兩個節曲線純滾動原理精確計算,因此,加工方法要復雜的多,目前還沒有查到相關的文獻。
理論上需要五軸機床才能完成: 除了銑刀盤的軸向( z) 移動和繞軸轉動,還需要橫向( x) 、縱向( y) 移動,以及被切輪坯的繞軸轉動和由節錐角變化引起的轉動。如已知非圓錐齒輪節曲線,就可以根據嚙合原理進行得到其加工方法。因此,求出一系列實時的銑刀盤位置 xi、yi、zi和被切輪坯的輪軸角度 αi以及繞軸轉角 φi,節錐角減去根錐角即是被切輪坯加工時輪軸的角度,根據這些參數控制五軸機床在各個自由度的運動配合,達到正確加工所設計的非圓形錐齒輪的目的。另外,還需要求得每個齒的初始位置、結束位置和中間間隔步長的每個位置,因此,要根據弧齒的螺旋角大小求得弧齒非圓形錐齒輪的加工參數。
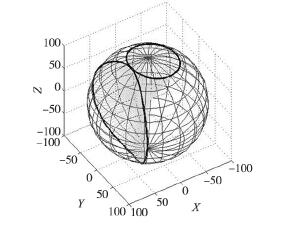
圖 2 一對嚙合的非圓錐齒輪節曲線
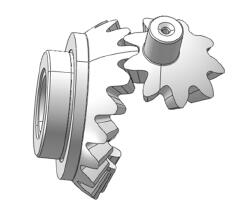
圖 3 直齒非圓錐齒輪
2. 1 弧齒非圓錐齒輪的螺旋角
弧齒錐齒輪輪齒的傾斜程度由螺旋角 βi來衡量。弧齒錐齒輪縱向齒形為節平面與輪齒面相交的弧線,該弧線稱為節線,平面齒輪的節線稱為齒線。節線上任意一點的切線與節錐母線的夾角稱為該點的螺旋角βi。通常把節線中點的螺旋角定義為弧齒錐齒輪的名義螺旋角 β,如圖 4a 所示。
弧齒錐齒輪副在正確嚙合時,大小輪在節線上除了有相同的壓力角之外,還要具有相同的螺旋角。
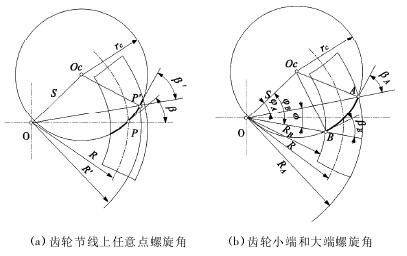
圖 4 弧齒非圓形錐齒輪的齒線與螺旋角

2. 2 假想平頂齒輪和齒輪坯單齒對應弧長
如圖 4b 所示,根據幾何關系,切制單個齒轉過角度見式( 4) :

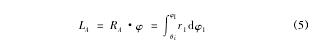
式中,下標為 1 的變量表示主動輪變量。對于與其嚙合的大齒輪,滾過弧長與小齒輪相等,可以用式( 5) 求得的值。
2. 3 銑刀盤位置
對于非圓齒輪,假設假想平頂齒輪的半徑和非圓齒輪的球面半徑相等,則其中心位置 O 是與錐齒輪重合的,也是固定的,盤銑刀的位置 Oc會隨著假想平頂齒輪的轉動而轉動,如圖 5 所示,瞬時位置為可求得如式( 6) 所示:

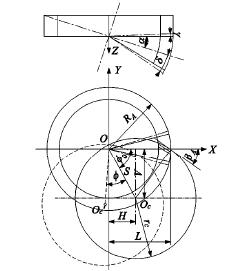
圖 5 假想平頂齒輪與銑刀盤關系
式中,V、H、T 為 Oc 相對于 O 點 3 個方向的距離; rc為刀盤最大半徑; βA為大端螺旋角。L = r0,r0為錐齒輪大端的球半徑; δ 為節錐角; γ 為根錐角; θi為被切齒輪任意位置 i 時的繞軸轉角。切某個齒時,從大端到小端,使該齒必須處于水平線位置。輪坯從起始位置開始,隨著輪坯轉過微小角度 Δφ( 第 j 個齒最大轉角為 φj) ,假想平頂齒輪也轉過對應的微小角度 ΔΦ( 第 j 個齒最大轉角為 Φj) ,φ 和Ф 由式( 7) 求得。
如圖 3 所示,銑刀盤初始位置與假想平頂齒輪中心距離用 S 表示,角度用 Ф0表示,則:
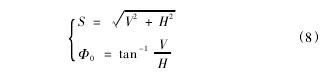
設輪坯勻速轉動,轉過角度 φ ,則對應的平頂齒輪轉角為 Ф,二者關系如式( 9) ,下標 1,2 表示兩個齒輪( 被切齒輪和假想平頂齒輪) 。
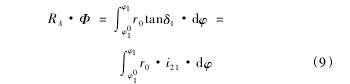
銑刀盤的瞬時位置如式( 10) 。可見,根據大端節曲線,可以求得加工銑刀盤位置坐標。
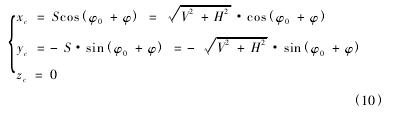
2. 4 NC 加工坐標變換
由于銑刀盤坐標系并不是數控機床的坐標系,而且還需求得被切輪坯轉角參數,因此,為數控編程和對刀,需要找到銑刀盤、被切輪坯和數控機床坐標系之間的關系,將坐標系平移轉換到數控機床的坐標系XWOWYW。圖 6 為銑刀盤、被切輪坯位置和數控機床坐標系關系,由圖 6 中坐標關系可得式( 11) ,通過式( 11)可求得銑刀盤一系列瞬時位置坐標( xW,yW,zW) ,用以控制銑刀盤運動,同時配合對應被切輪坯瞬時軸轉角 α( 節錐角 δ 與根錐角 γ 差值) 和繞軸轉角 φ,即可加工出弧齒非圓錐齒輪。
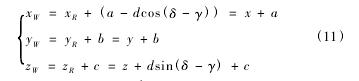
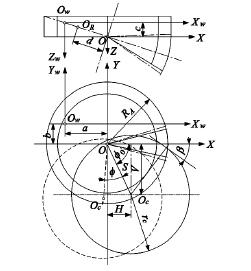
圖 6 銑刀盤、被切輪坯和數控機床坐標系關系
被切輪坯加工參數為軸轉角和繞軸轉角,角度值與坐標平移無關,故保持不變。
3 、弧齒非圓錐齒輪數控銑削加工實例
利用上述方法對弧齒非圓錐齒輪進行數控加工坐標計算,齒輪節曲線如圖 2 所示。加工相關參數為: RA= 46.6mm,RB= 34.6mm,rc= 88.9 /2 mm,小齒輪齒數 N = 12,螺旋角 β = 35°,齒厚 b = 12mm。

表 1 部分銑刀盤位置坐標和被切輪坯角度值
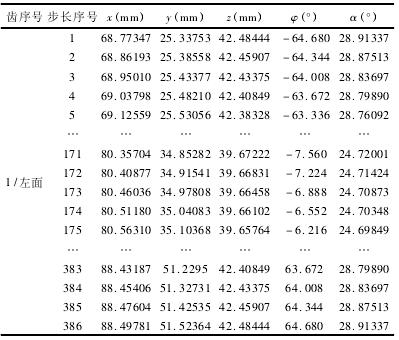
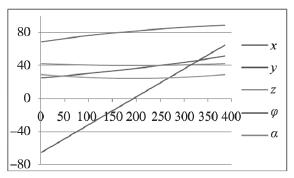
圖 7 第一齒單面加工時各參數坐標曲線
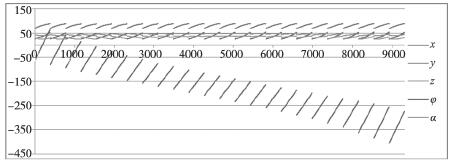
圖 8 小齒輪 12 個齒全部加工時各參數坐標曲線
根據上述方法,利用五軸數控機床分別切削加工一對嚙合的非圓錐齒輪樣品,主要參數為: 齒輪外球面直徑 46.6mm,大齒輪齒數 24,小齒輪齒數 12,成型盤銑刀模數 3.5,刀盤半徑 44.3mm,弧齒螺旋角 35°。圖9 為利用本文方法加工完成的一對弧齒非圓形錐齒輪,與設計的齒輪參數一致。且兩齒輪能夠正確嚙合,說明本文加工方法正確有效。

圖 9 加工完的弧齒非圓形錐齒輪嚙合
4 、結論
根據非圓錐齒輪的節曲線數據和齒輪嚙合理論,推導了利用成型盤銑刀數控加工弧齒非圓錐齒輪的公式,計算一系列盤銑刀和被切輪坯的瞬時位置,作為數控加工程序的控制參數,經過齒形修正,可用五軸數控機床加工弧齒非圓錐齒輪。基于本文方法加工出來的一對非圓錐齒輪可以正確嚙合傳動,證明該方法可行,與線切割方法和點火化加工方法比較,提高了加工精度和加工效率。
作者:孟祥德 張學玲 張俊紅
來源: 天津大學仁愛學院 機械系, 天津捷強動力裝備股份有限公司 天津大學機械工程學院
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com




