基于數字孿生技術的五軸聯動坐標轉換
2020-9-17 來源:中國科學院寧波材料技術與工程研究所等 作者:秦秀,張文武,茹浩磊,張天潤,王吉
摘要: 針對現有坐標變換公式計算繁瑣且容易出錯的問題,將數字孿生技術應用到五軸聯動設備的坐標變換過程中。在 NX 軟件中搭建了五軸設備的精準零部件模型,并將模型導入 Simscape/Multibody 模塊進行了多剛體物理建模。創建五軸聯動設備的數字孿生模型后,開展坐標變換仿真,并運用公式計算驗證了仿真模型的正確性。
關鍵詞: 數字孿生; 五軸聯動; 坐標變換
1、引言
數字孿生是指針對物理世界中的實體,通過數字化的手段來構建一個數字世界中一模一樣的實體,以模擬其在現實環境中的行為,并對過去和現在的行為或流程進行動態呈現,有效反映系統運行情況,從而對不可預測的情況進行更加真實和全面的檢測。
數字孿生( Digital Twin) 的概念最早可追溯到2003 年,美國密歇根大學的 Michael Grieves 教授在其 PLM( 產品生命周期管理) 課程上提出“與物理產品等價的虛擬數字化表達”的概念。受限于當時的數據采集技術、數字化描述技術、計算機性能以及算法,數字孿生概念和模型在 2003 年提出時并沒有引起國內外學者們的重視。2011 年后,數字孿生迎來了新的發展契機。2011 年,數字孿生( Digital Twin)一詞由美國空軍研究實驗室( AFRL,Air Force Re-search Laboratory) 提出并希望利用數字孿生來解決戰斗機機體( Airframe) 的維護問題。
數字孿生近期得到了廣泛關注。全球最具權威的 IT 研究與顧問咨詢公司 Gartner 連續兩年( 2016年和 2017 年) 將數字孿生列為當年十大戰略科技發展趨勢之一。世界最大的武器生產商洛克希德馬丁公司于 2017 年 11 月將數字孿生列為未來國防和航天工業 6 大頂尖技術之首; 2017 年 12 月 8 日中國科協智能制造學術聯合體在世界智能制造大會上將數字孿生列為世界智能制造十大科技進展之一。
五軸聯動編程是在 NX/CATIA/Pro Engineer 等加工軟件中進行刀路軌跡規劃并輸出刀軌文件。在刀軌數據中,包含 3 個相對于工件坐標系的 X、Y、Z坐標值和 3 個 I、J、K 刀軸矢量。其中,坐標值表達了虛擬刀尖相對于工件坐標系的位置,刀軸矢量表達了刀軸相對于工件坐標系的方向,這 6 個數據可以確定加工軌跡。但在機床坐標系中,機床所參照的坐標有 5 個,即 X、Y、Z 三個坐標值和 A、B、C 之中任意兩個轉角。因此,五軸坐標變換的實質是將刀軌數據的坐標值和刀軸矢量轉換為機床坐標系的坐標值和轉角值。
2、五軸聯動設備的數字化設計
2. 1 基于數字孿生的五軸聯動坐標轉換
現在的五軸坐標轉換流程是根據設備運動特點來確定設備的運動鏈,計算各個環節的變換矩陣,建立方程進行求解,得到不同坐標系轉換之后的坐標點。但該方法計算繁瑣且容易出錯。基于數字孿生的五軸聯動坐標轉換思路如下: 建立五軸聯動設備的三維數字模型,該模型應包含每個機械零件的外形尺寸、幾何公差及裝配位置關系等; 在數字仿真模型中添加運動副,確保仿真模型與物理模型有相同的運動關系; 根據五軸聯動設備的真實坐標零點來確定三維數字模型的坐標零點。這種方法中,設定數字模型中各部件坐標軸位置關系的過程就是實施坐標轉換的過程,因此,運行仿真過程即可得到轉換后的坐標點。
2. 2 機械結構三維建模
五軸數控機床一般存在 3 個線性運動軸和 2 個旋轉 運 動 軸。兩 旋 轉 軸 位 置 不 同,結 構 千 差 萬別。本文以 X、Y、Z、A、B 軸機床為例,開展基于數字孿生技術的五軸聯動坐標轉換技術研究。如圖1 所示,設備由沿著 X、Y、Z 三個方向移動并平行于X 軸轉動的 A 軸以及平行于 Y 軸擺動的 B 軸組成。A 軸的運動范圍為 0° ~ 360°,B 軸的運動范圍為- 90° ~ + 90°。
2. 3 創建 Sims cape 仿真模型
Simscape 是由 MathWorks 公司推出的一種基于物理模型的綜合建模平臺,現已廣泛用于機械、液壓、電子電力行業建模。Simscape 采用物理網絡的方法進行模型構建,模塊相當于物理元器件,連接線相當于可用于能量傳遞的物理連接,因此更接近于真實的物理模型。
Simscape / Multibody 提供適用于 3D 機械系統的多體仿真環境,可以使用表示剛體、關節、約束、力元件和傳感器的模塊對多體系統進行建模。通過Simscape,可以基于物理連接直接相連模塊框圖來建立物理組件模型。
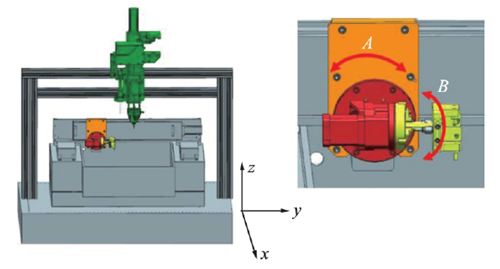
圖 1 NX 中創建的設備三維模型
本文利用 Simscape Multibody 模塊建立了五軸聯動設備的模型( 見圖 2) 。其中,Rigid Transformblock 為類似于坐標變換的剛性變換模塊,可以對左右兩個端口的 frame 進行旋轉和平移變換。RigidTransform block 是定向的,有 B 和 F 兩個端口,且 B和 F 總是相對的,即 B 是變換前的坐標系,F 是變換后的坐標系。旋轉變換包含與軸對齊( Aligned Ax-es) 、對軸的角度旋轉 ( Standard Axis) 、任意軸旋轉( Arbitrary Axis) 、旋轉序列( Rotation Sequences) 和旋轉矩陣( Rotation Matrices) 選項,見圖 3a; 平移變換包含笛卡爾坐標或圓柱坐標系下的向量偏移以及沿標準軸的位移偏移,見圖 3b。如果旋轉和平移均為 None,那么這兩個 frame 在空間上重合,相當于用鏈接線直接將兩個 frame 連接在一起,即一個沒有剛性變換的 block。
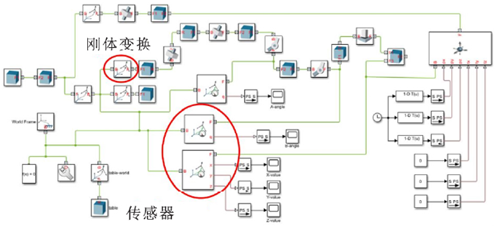
圖 2 Simscape Multibody 中五軸聯動設備模型

圖 3 剛性變換模塊設置
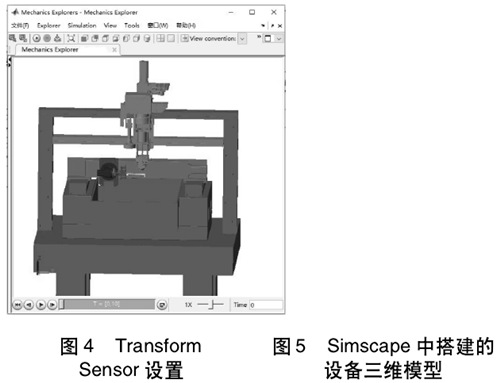
Transform Sensor block 可以測量兩個剛體或兩個坐標系之間位置關系。測量時,B 口連接基坐標系,F 口連接想要測量的坐標系,見圖 4。搭建好的設備三維模型見圖 5。

2. 4 坐標零點擬合
根據五軸聯動設備的實際坐標零點,設定仿真模型的坐標零點,并與世界坐標系( World Frame) 相連接,確保數字孿生模型與物理設備的高度一致性。根據模型與世界坐標系的連接關系確定虛擬模型的坐標零點,見圖 6。
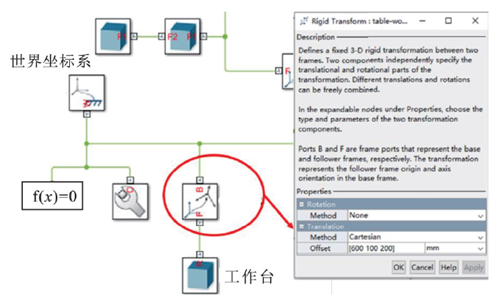
圖 6 坐標零點擬合
3、五軸聯動運動仿真
為保證仿真模型與物理設備的高度一致性,需將物理設備的實測誤差補償到仿真模型。
取工 件 坐 標 系 中 坐 標 點 ( - 33. 5,25. 7,- 4. 3) ,該點在曲面上的法向矢量為 ( - 0. 4281,0. 0045, - 0. 9038) 。在機床加工過程中,由于機床主軸為 Z 軸,所以需要通過機床提供 A、B 兩個方向的旋轉運動,將工件上該坐標點的法向矢量旋轉到與 Z 軸平行。在仿真模型中,以工件的運動軌跡為輸入,運用逆向運動學求解,測量 A、B 軸的轉角與旋轉之后的 X、Y、Z 坐標值,見圖 7。仿真后,X =2. 596,Y = - 112. 582,Z = 56. 975,A = 0. 28°,B =- 89. 4°。
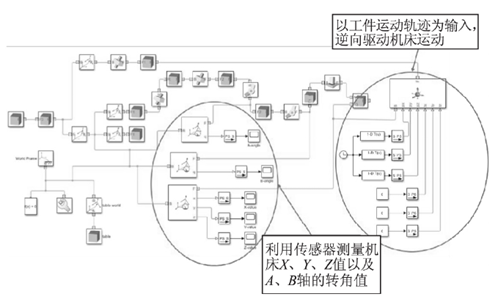
圖 7 運動仿真模型
4、仿真結果驗證
為了驗證仿真結果是否正確,可利用公式計算對仿真結果進行驗證。根據設備的運動鏈,建立機床坐標系 Om、工件坐標系 Ow以及旋轉坐標系 Oa之間的關系,見圖 8。
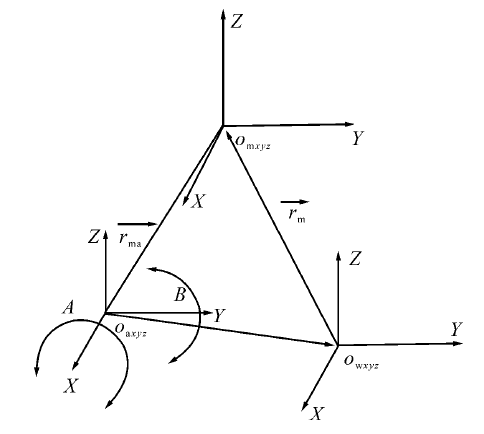
圖 8 坐標系位置矢量關系
在工件坐標系中取曲面坐標( - 33. 5,25. 7,- 4. 3 ) ,曲 面 在 該 點 的 單 位 法 向 矢 量 r =( - 0. 4281,0. 0045,- 0. 9038) 。由于機床主軸為 Z軸,因此,必須使 r 與 Z 軸重合才能加工該點。為此,在機床提供 A、B 兩種旋轉運動的前提下,工件要繞 B 軸和 A 軸做兩次旋轉才能滿足要求。計算旋轉后的坐標點就是計算這兩次旋轉的角度以及旋轉后的 X、Y、Z 坐標值。
工件旋轉之前應先平移到旋轉坐標系下( A 軸與 B 軸的交點處) 。平移變換矩陣為[- 24,- 138,7. 5],平移后的坐標值為( - 57. 5,- 112. 3,3. 2) 。
繞 B 軸旋轉 θ 角度,θ = arctanij= - 89. 3977°。則有
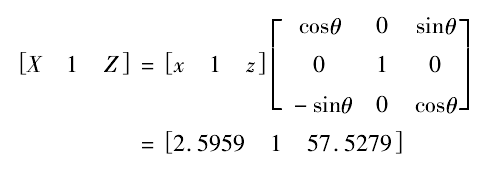
旋轉后 Y、J 值保持不變,I = 0,K = 1 - J槡2=0. 99998。
繞 A 軸的旋轉角度 α = arctanik= 0. 2821°,則有
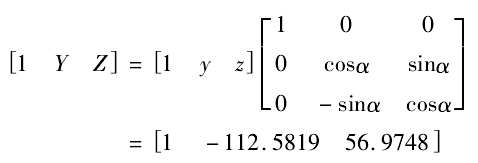
旋轉后 X、I 值保持不變,J = 0,K = 1。
因此,旋轉變換之后的坐標變為 X = 2. 5959,Y = - 112. 5819,Z = 56. 9748,I = 0,J = 0,K = 1。
上述計算結果驗證了仿真模型的正確性。
5、結語
本文基于數字孿生的技術原理,在 NX 軟件中對五軸設備進行了精準建模,將模型導入 Simscape /Multibody 中進行了多剛體物理建模,按照設備實際情況添加運動副,并設定坐標零點,保證了仿真模型與設備的高度一致性。利用仿真模型開展了坐標變換仿真,并用傳統的公式計算對仿真結果進行了驗證分析。結果表明,公式計算與仿真分析的結果一致,證明了利用虛擬模型開展坐標變換的可行性。
目前,國內外基于數字孿生技術開展坐標變換的案例很少。本文驗證了這一技術思路的可行性,有利于數字孿生技術的推廣和應用。同時,該項技術可為基于數字孿生技術開展后處理編程與仿真提供技術基礎。
參考文獻
[1]陶飛,劉蔚然,劉檢華. 數字孿生及其應用探索[J]. 計算機集成制造系統,2018,24( 1) : 1 - 18.
[2]Qinglin Qi,Fei Tao,Tianliang Hu,et al. Enabling technolo-gies and tools for digital twin[J]. Journalof ManufacturingSystems. Available online 29 October 2019.
[3]Qianzhe Qiao,Jinjiang Wang,Lunkuan Ye,et al. Digital twin for machining tool condition prediction[C]. 52nd CIRP Con-ference on Manufacturing Systems,Procedia CIRP,2019,81:1388 - 1393.
[4]Yuqian Lu,Chao Liu,Kevin I-Kai Wang,et al. Digital twin-driven smart manufacturing: connotation,reference model,applications and research issues[J]. Robotics and Computer Integrated Manufacturing,2020,61: 101837.
[5]Chenyuan Zhang,Wenjun Xu,Jiayi Liu,et al. A reconfigu-rable modeling approach for digital twin based manufacturing system[J]. Procedia CIRP 2019,83: 118 - 125.
[6]鄭惠強,郝一舒,李愛紅. 五軸銑削加工中心坐標轉換數學模型的建立及應用[J]. 計算機應用與 IT 技術. 2004,25( 1) : 27 - 29.
[7]Mihai Crenganis,Melania Tera,Cristina Biris,et al. Dynamic analysis of a 7 DOF robot using fuzzy logic for inverse kine-matics problem[J].ProcediaComputer Science,2019,162:298 - 306.
[8]王安邦,孫文彬,段國林. 基于數字孿生與深度學習技術的制造加工設備智能化方法研究[J]. 工程設計學報,2019,26( 6) : 1 - 9.
[9]杜澎,董佑浩,苗盛. 非正交五軸聯動數控機床后置處理算法開發[J]. 數控技術,2019( 12) : 160 - 164.
[10]呂強. UCP710 五軸機床中的坐標轉換[J]. CAD/CAM與制造業信息化,2003( 4) : 87 - 94.
[11]林蓮. 基于 MATLAB/Simulink/Sim Scape 的無刷直流電機的建模與仿真[J]. 裝備制造技術,2018 ( 8) : 138 -141.
第一作者: 秦秀,碩士,工程師,中國科學院寧波材料技術與工程研究所,浙江省寧波市 315201
通信作者: 張文武,研究員,中國科學院寧波材料技術與工程研究所,浙江省寧波市 315201
作者: 秦秀,張文武,茹浩磊,張天潤,王吉
來源: 中國科學院寧波材料技術與工程研究所; 浙江省航空發動機極端制造技術研究重點實驗室
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息





