【技術淺析】數控機床軸承結構振動諧響應及疲勞壽命研究
2020-11-9 來源:貴州師范大學 機械與電氣工程學院等 作者:沈明明,李榮,劉祖國,湯耿
摘要: 以數控機床用的深溝球軸承為研究對象,分析其運轉中的振型及結構疲勞壽命。首先通過Solidworks 建立了深溝球軸承的三維模型,利用ANSYS 對軸承進行模態及諧響應分析,獲得軸承在固有振動頻率以及在各階次頻率下的固有振型變化,同時借助有限元諧響應分析,確定了對軸承影響最大的模態頻率。其次利用 ANSYS 中的 Faigue 模塊對軸承進行了疲勞壽命研究,通過結合材料的 S-N 曲線理論以及 Hertz 接觸理論,對軸承的疲勞壽命進行了預估分析。仿真結果表明: 在滿足軸承強度工況下,固有頻率 1125Hz 為結構共振最大點,且軸承的壽命范圍為5937. 7 ~ 1 × 106次,為后續軸承結構優化提供參考。
關鍵詞: 深溝球軸承; 模態振型; 振動諧響應; 疲勞敏感性; 疲勞壽命
0、引言
隨著制造工業技術的快速發展,數控機床被廣泛應用于關鍵零部件的加工制造,而主軸系統中軸承結構則是其運轉的關鍵部件。軸承作為重大機械傳動中的重要支承傳動部件并且能夠減少摩擦,因此軸承的好壞直接關系到機床加工精度和工作效率等性能。
同時軸承的振動疲勞破壞一直是影響機械結構運行的關鍵因素。近幾年,國內外學者對軸承結構的運行狀態及振動變化進行了研究分析,文獻通過利用有限元法對航空圓柱滾子軸承的溫度場及應力分布進行仿真分析同時還對軸承熱力耦合下的疲勞壽命進行研究,文獻通過建立接觸模型,提出了一種載荷計算分布模型對深溝球軸承內部載荷序列與壽命進行計算。文獻中HOUPERT 分析了滾動軸承在運行過程中對疲勞壽命造成影響的因素,上述研究都取得了一定的效果,但都只是單一的針對軸承的溫度場及載荷序列進行研究。針對軸承振動諧響應與壽命的研究的報道并不多。
因此,本文以數控機床用深溝球軸承為研究對象,通過對軸承結構進行參數化建模,分析軸承靜應力及模態振型變化。結合諧響應分析模塊,利用模態疊加法分析深溝球軸內圈的諧響應變化。同時利用材料的S-N 曲線及疲勞靈敏度曲線對軸承進行了恒定載荷工況下的疲勞壽命研究,為數控機床主軸系統軸承振動疲勞分析及優化提供了參考。
1、深溝球軸承有限元分析
1.1、深溝球軸承靜應力分析
軸承結構在運行過程中其結構的振型變化將會直接對結構的性能造成一定的影響,因此結構的振動特性決定了結構在不同載荷情況下的響應變化,所以對結構進行模態振型仿真分析具有重要意義。
由于在 ANSYS 中的建模工具并不成熟,因此本文利用 Solidworks 建立了深溝球軸承的參數化三維模型,通過轉變模型的格式聯立到 ANSYS 中進行分析,在進行分析時需要對結構的材料進行定義,本文分析時主要是利用有限元的方法進行利用,因此本文設定結構的材料都為軸承鋼,其泊松比 為 0.3,密度為7810kg/m3,彈性模量為210GPa,設定完材料參數后,需要對結構的網格進行定義,因為在仿真分析時結構的網格是否合格直接影響到結構的分析精度,雖然系統有手動劃分網格的功能,針對復雜的幾何結構大多采用自動劃分功能,通過設定網格為 Fine 劃分得到如圖 1 所示的深溝球軸承有限元網格模型,其中網格節點為10536,單元數為3950,網格質量為良好。
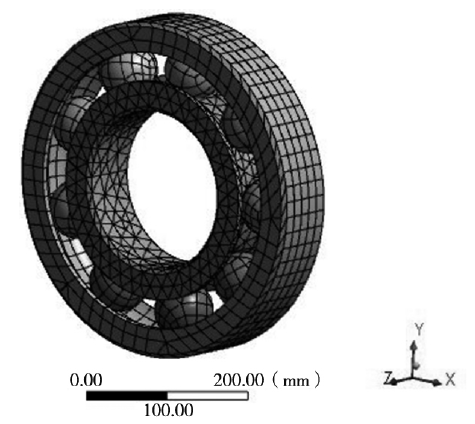
圖1 . 深溝球軸承有限元網格模型
1.2、邊界條件設定
在軸承運行過程中,其中內圈是與轉子軸接觸,外圈則一般是與固定件接觸在一起,因此在設置深溝球軸承約束條件時將圖 1 中軸承外圈設定為固定約束,內圈設定為旋轉約束,本文轉速設置為10000rpm。
1.3、有限元靜應力結果
通過設定完結構的邊界約束條件和網格模型后,在靜應力模塊中選中變形模塊及平均應力模塊,分析解算得到如圖 2a 所示的靜應力總變形和圖 2b 所示的軸承平均應力云圖。
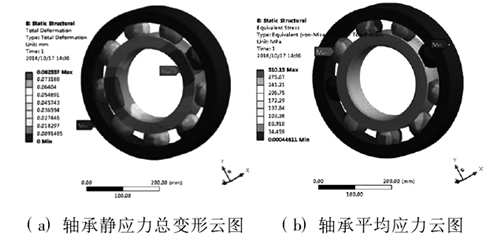
圖2 . 軸承靜應力應變形云圖
從圖 2 中的云圖可知,深溝球軸承的最大變形量為 0.083mm,軸承的最大平均應力為 310MPa,由于在設定材料時,定義的軸承材料為是軸承鋼,彈性模量為210GPa,屈服強度為 1667MPa。根據第 4 強度理論可以計算材料是否符合強度要求,強度公式為:
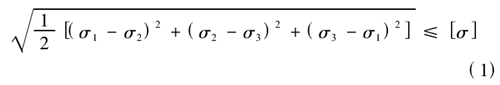
式中,σ1,σ2,σ3為 3 個法向的應力。在計算材料的許用應力時,安全系數一般取的是 1.5,通過許用應力公式計算可得到。許用應力公式:

通過結合式( 1) 與式( 2) 可以計算軸承的許用應力為 1111.3MPa。結合圖 2 應力云圖可得 310MPa≤1111.3MPa,所以創建的軸承結構的強度滿足設計分析要求。因此在后續的諧響應分析及疲勞壽命的分析中可以獲得軸承具有參考價值的數據參數,為后期軸承的改進提供有效的優化方案。
1.4、深溝球軸承模態分析
在繪制深溝球軸承結構的三維模型時,忽略掉一些對結構影響不明顯特征,這樣將能加快求解時間。由于軸承產生破壞的階段主要是在負載工況下發生的,所以本文在繼承靜應力分析的基礎上對軸承的模態振型進行研究分析。設定模態階數為 6 階,得到軸承的前 6 階模態固有頻率如表 1 所示。
表 1 深溝球軸承前 6 階振型

結合 1.1 節的模態有限元分析可知,結構在運轉過程中,主要是低階模態的振型對結構的破壞較為關鍵,因此在有限元分析時不需要考慮到高階模態的振型,因此選取了軸承的前 6 階進行模態振型分析,模態分析結果如圖 3 所示。
從圖 3 中模態振型變化中可以得到,軸承的低階模態振型變化量較大,主要對內圈的軸向振動變形較為明顯,其中在模態 2 階中振動變形達到最大,最大約為 20mm,可以判定在內圈與滾珠接觸的部位較為薄弱,為提高軸承的可靠性及壽命可以在與軸承的內圈與滾珠接觸部位提高加工精度或對滾道進行特殊處理,以提高滾道的光滑度及強度。對此在本文的后續諧響應分析中主要對軸承結構的內圈進行分析,為后續軸承結構的優化及加工提供參考。
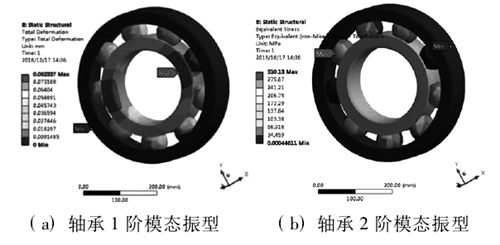
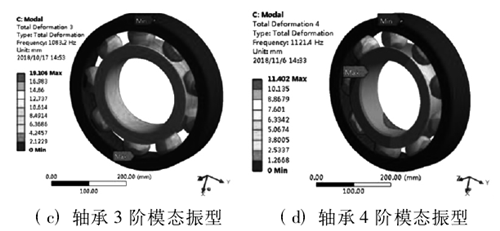

圖3 . 深溝球軸承前6階模態振型云圖
1.5、深溝球軸承諧響應分析
結構的諧響應分析主要是對載荷在不同頻率下的振動響應,直接與結構的載荷有關,而模態分析的結果只是單一的獲得在某一頻率下的振型變化,并不能獲得在不同頻率下的變形。因此結合模態分析結果搭建諧響應分析來提高諧響應分析結果的可用性,同時通過諧響應分析還可為軸承的疲勞破壞和共振破壞具有一定預測作用,對此本文通過模態疊加法開展軸承結構的諧響應分析,在求解中的設置條件為:
① . 設置軸承的邊界條件參考 1. 2 節中的條件。
② . 從圖 3 的模態云圖和表 1 中的前 6 階固有頻率可知,軸承的第6階頻率為 1285.3Hz,對此設置諧響應的分析范圍為0~1500Hz,同時為了提高計算結果的精確性設置求解步數為 100 步對應的有100個解。由模態分析可知變形主要發生在軸承的內圈,因此在諧響應分析中主要選取內圈進行了諧響應分析,通過求解計算獲得了內圈沿 X、Y、Z 方向的位移變化情況,如圖4所示。
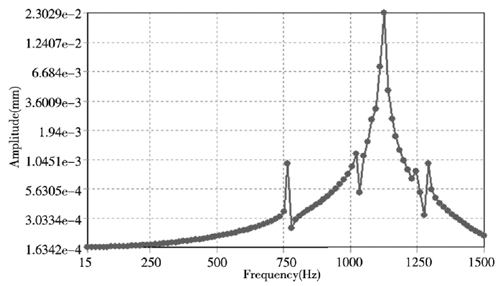
(a) X 方向
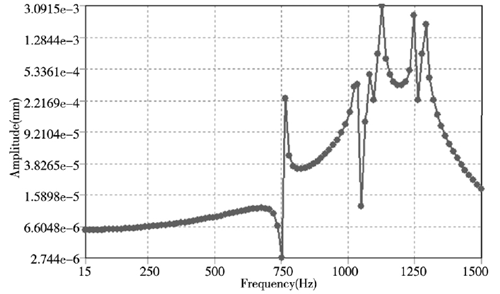
(b) Y 方向
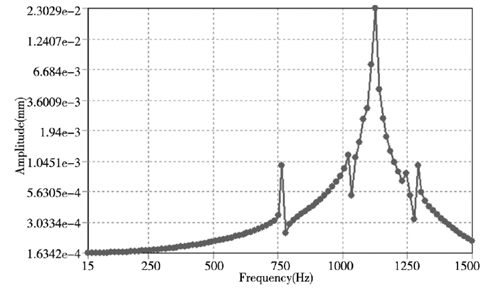
(c) Z 方向
圖4 . 軸承內圈結構 X、Y、Z 方向位移響應曲線
從圖 4 中的軸承內圈結構 X、Y、Z 方向位移響應曲線可知,軸承結構的位移響應隨著頻率的增加而增加,呈正相關。而在 X、Z 方向的位移在模態 5 階( 約1125Hz) 時達到最大位移變化,最大變化量為0.023mm,而對于Y方向的位移變化量則較小為0.003mm,這要是軸承在 Y 方向上主要是受到徑向的力,而 X 和 Z 方向還會受到沿 X 軸的軸向力,因此在 X和 Z 方向的位移較大,雖然 Y 方向的最大位移量沒有X 和 Z 方向的大,但在頻率從1階到 6 階范圍內位移變形量較為均勻,因此造成的破壞不容忽視。通過對軸承的諧響應的分析可知 X、Y、Z 方向所造成的影響都不可忽視,在后期優化和加工工藝中通過設計特定的工裝來優化軸承的結構,諧響應分析結果也為后期同類產品的優化提供參考。
2、深溝球軸承疲勞壽命分析
2.1、Hertz 接觸應力計算
在分析軸承應力疲勞壽命時,應先分析軸承的應力,同時找到軸承的最大應力區域。對此依據 Hertz接觸應力理論對軸承的應力進行分析,在接觸應力中接觸載荷 Q 與彈性趨近量 δ 滿足下式:
式中,K 代表接觸體之間的載荷變形系數,一般與接觸體的材料及外形有關。
在軸承工作過程中,由于內外滾道的直徑差異,滾道對滾珠的接觸應力也有所不同,同時 2 滾道的法向趨近量等于滾珠分別與內外滾道趨近量之和,滿足下式:
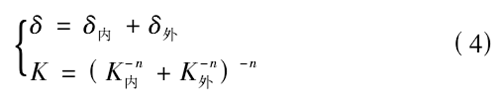
對于深溝球軸承,式( 3) 和式( 4) 中的 n 系數一般取 1.5。通過 Hertz 理論分析球軸承的接觸問題,其最大的接觸應力為:

式中,a 表示接觸橢圓的長半軸; b 表示接觸橢圓短半軸。
通過上式理論分析在結合圖 2 所示的靜應力仿真分析云圖可知,接觸處的正壓力主要為滾珠與內外圈接觸部位,其值沿曲面軸向與法向變化,與式( 5) 的接觸理論分析一致。
2.2、疲勞分析
采用 ANSYS 聯合仿真對深溝球軸承進行疲勞計算,在分析軸承靜應力的基礎上聯合 Faigue 模塊進行分析,在分析設置中為了提高分析的有效性,在搭建的Faigue 模塊中設置疲勞強度因子為 0.8,通過反復模擬分析取最小基本載荷變化幅度和最大基本載荷幅度分別為 10% 、300% ,由此獲得軸承結構的疲勞敏感性曲線如圖 5 所示。
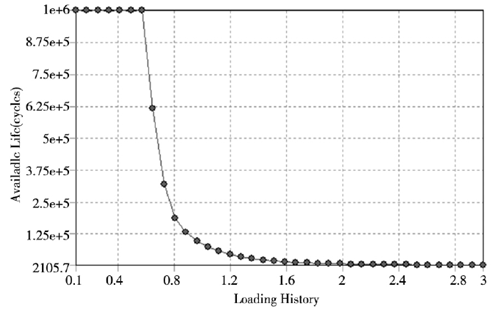
圖5 . 深溝球軸承疲勞敏感性曲線
在設定軸承的疲勞安全因子分布云圖命令,可獲得如圖 6 所示的安全因子分布云圖。從圖 6 中可以得到,本文選取的深溝球軸承最小安全影響因子為0.27795,最容易發生疲勞破壞的部位主要是軸承內圈,這與實際工況下的破壞一致,為提高壽命,在后續的優化設計可以改變內圈材料及內圈與滾珠接觸處的尺寸參數來提高軸承內圈的使用壽命。由圖 5 中的敏感性曲線可知,軸承在載荷變化幅度為 10% ~ 60% 范圍內對軸承的壽命影響不大,但在載荷變化幅度超過200% 時則直接對軸承造成破壞不滿足設計要求,通過上述分析可為軸承在設計中驗證軸承疲勞壽命是否滿足要求提供參考。
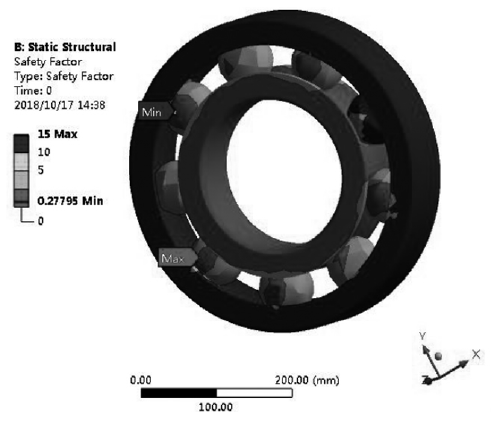
圖6 . 深溝球軸承安全因子云圖
2.3、振動疲勞壽命計算
一般情況下軸承的循環壽命較高,屬于低應力高周疲勞,通過采用全壽命分析方法,即 S-N 曲線對軸承進行疲勞壽命分析計算,通過上述的對軸承的材料進行定義得到軸承的 S-N 曲線如圖 7 所示。
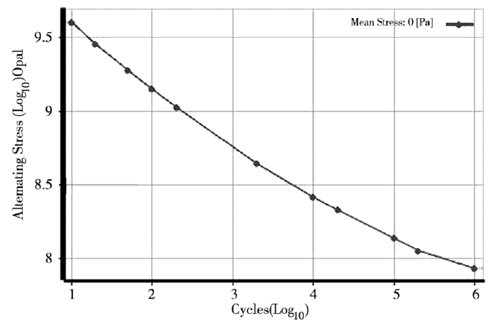
圖7 . 軸承 S-N 曲線
在有限元分析中,設置雨流循環計數的方法對不規隨機的載荷時間歷程曲線進行轉化成一系列恒定幅值的載荷,本文設定的載荷為恒定幅值載荷對軸承進行疲勞壽命預估,如圖 8 所示。
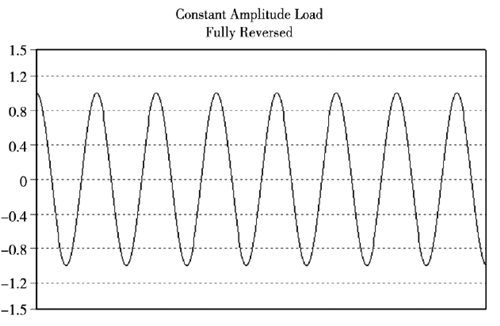
圖8 . 恒定幅值載荷
其中疲勞壽命公式如下:
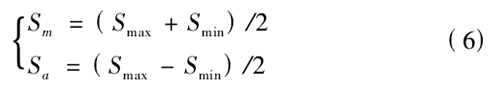
式中,Sm表示平均應力; Smax表示最大應力取310MPa; Smin為最小應力取 34MPa; Sa表示交變應力幅。
其中平均應力的修正應力公式為:

式中,Sn為平均應力 Sm的修正應力;
由圖 7 所示的軸承 S-N 曲線來計算曲線間的斜率h,可以假設 S* N = C 為直線,利用最小二乘法來擬合出最優的直線方程,擬合得到如下方程:
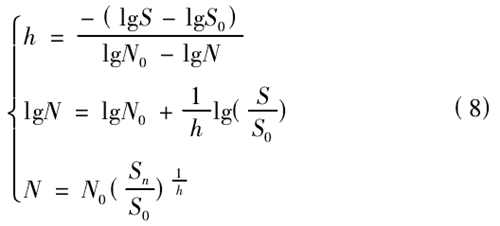
式中,N0表示循環次數,N0= 1 × 106; S0表示在 N0=1 × 106時的應力;
結合圖7可知 lg N0= 6,lg S0= 7.88,lg N = 3,lg S = 8.75 ,通過計算可得到 h 值為 - 0.29。其中平均應力 Sm的修正應力為:Sn=153.8MPa 將其帶入式(8) 中可得軸承疲勞壽命 N≈8.74 × 104次。結合圖5的敏感性曲線圖可知軸承的載荷變化幅度在 10% ~60% 范圍內,因此對軸承的壽命影響不大,滿足疲勞壽命設計要求。
同時借助有限元 Faigue 分析模塊,對深溝球軸承循環次數的疲勞壽命進行求解計算,可獲得圖 9 所示的軸承疲勞壽命云圖。

圖9 . 深溝球軸承疲勞壽命( 循環次數)
由圖 9 中的疲勞壽命分析云圖可知,當工況條件為轉速設置 10000rpm 時,軸承的壽命范圍為 5937.7 ~1×106次,壽命較小處為軸承的滾珠外側和軸承內圈部位,但是壽命薄弱處較少,其有限元疲勞壽命分析與理論計算結果大體一致,且有限元分析法能夠將疲勞破壞點清晰直觀的表示出來,由此可知通過利用有限元法對結構做疲勞壽命分析是可靠的,可為后續結構優化提供參考。
3、結 論
深溝球軸有限元靜應力及模態分析,能獲得結構的固有頻率及振型變化,可為結構的諧響應及疲勞分析提供基礎。
(1)、結合有限元靜應力及模態分析結果,采用模態疊加法,搭建了軸承結構的諧響應分析模塊,獲得了軸承內圈沿 X、Y、Z 方向上的位移響應曲線,得到了軸承在 X、Z 方向的位移在模態 4 階( 約1125Hz) 時達到最大位移變化,最大變化量為 0.023mm;
(2)、通過利用材料的 S-N 曲線理論以及 Hertz 接觸理論開展了軸承結構的疲勞壽命分析,在靜應力分析的基礎上,通過 Faigue 模塊建立軸承結構的疲勞分析模型,理論疲勞壽命為 8. 74 × 104次,與仿真分析結果大體一致,驗證了仿真計算的可行性,也為軸承結構的后續優化提供參考,加快研發進度。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息





