基于Archard 理論的滾珠絲杠磨損預測
2016-11-15 來源:東南大學 沙洲職業工學院 作者:徐向紅 湯文成 俞 濤 殷 銘
摘要:在數控機床等自動化設備中,滾珠絲杠副具有相對封閉結構特性。為了研究其磨損特性,基于Archard 模型的增量形式建立了滾珠絲杠副的磨損模型,并通過分析滾珠絲杠副運轉過程中的接觸變形和接觸角的變化,求出接觸點的相對速度。考慮到軸向載荷、接觸面間的相對速度、離心力和陀螺力矩的影響,推導出滾珠絲杠副磨損后的軸向位移,用數值方法得到了滾珠絲杠副的磨損規律,同時在試驗臺上進行了實驗驗證。實驗結果表明,在滾珠絲杠副運行中的黏著磨損階段,磨損模型的理論值與實測值吻合較好, 所建立的滾珠絲杠副磨損模型能夠反映黏著磨損階段的實際磨損變化規律。
關鍵詞:滾珠絲桿副;磨損模型;黏著磨損;磨損預測;Archard
0.引言
滾珠絲杠副在數控機床等自動化設備的系統中起著關鍵作用,由于滾珠與絲杠和螺母之間都是緊密接觸并有相對運動,運行中必然會導致磨損,使整個系統振動加大、精度降低。由于磨損現象復雜多樣,很難準確預測滾珠絲杠副的壽命,而試驗探索的代價較高,結果也不盡如人意。高速精密滾珠絲杠副的磨損問題已經成為國內急需解決的關鍵技術,嚴重制約了相關行業的發展,目前對于滾珠絲杠副的研究重點集中在運動學和動力學特征行為,而對摩擦磨損的研究還不深入,迫切需要加強這方面的研究,以提高國內精密數控機床的性能。
滾珠絲杠副中的磨損主要源自滾珠與絲杠和螺母滾道的滑動摩擦[1] 。由于滾道表面不同位置的線速度與到絲杠軸線的距離成正比,且滾珠在繞絲杠軸線旋轉的同時還相對接觸面的法線自轉,因此滾珠與絲杠和螺母滾道表面的接觸點上的線速度不可能完全相等,滾珠與滾道必然會產生相對滑動。由于滾珠絲杠副是個相對封閉的裝置,在工作中很難直接觀測內部參數的變化,必須借助運動學分析獲得相關參數,進而建立滾珠絲杠副的磨損與載荷、接觸面相對速度之間的關系[2-3] 。
滾珠絲杠裝置受力后產生的彈性變形會降低其動態傳動精度,陳勇將等人[1] 分析了微型滾珠絲杠副的摩擦機理,建立了微型滾珠絲杠副的摩擦力矩模型;Amin Kamalzadeh 等人[4] 依據動力學模型分析了彈性變形引起的行程誤差并建立了相關仿真模型;吳保群等人[5] 基于摩擦學理論建立了滾珠絲杠副摩擦系數與載荷、磨損率與載荷的簡化計算公式;Jui-Pin Hung 等人[6] 基于有限元分析法對滾珠與返向器之間的沖擊失效過程進行了分析與仿真;Chin ChungWei 等人[7] 分析了預載荷和潤滑條件對滾珠絲杠副摩擦力與機械效率的影響;Christian Brecher 等人[8] 研究了潤滑條件對滾珠絲杠副磨損過程和摩擦力的影響關系;A. Verl 等人[9] 研究了預緊力對滾珠絲杠副工作時的等效載荷與壽命的影響關系;Horng 等人[10] 建立了不同顆粒變形下的三體微接觸模型。
在磨損研究方面,Xiulin Sui 等人[11] 建立了球形端銑刀磨損數學模型以預測在銑削過程中刀具的磨損量;張詳坡等人[12] 采用組合磨損計算方法分別建立了自潤滑推力關節軸承和向心關節軸承的磨損壽命模型;鐘洋等人[13] 運用Archard 磨損理論分析了滾珠直線導軌副的磨損過程并建立滑塊位移的計算模型,用來預測滾珠直線導軌副的磨損量;Weijun Tao 等人[14]借助Archard 磨損理論分析了滾柱直線導軌的磨損過程;Xuejin Shen 等人[15] 基于Archard 磨損模型模擬了滑動軸承的非線性磨損過程;Mirbagheri,S. E 等人[16]建立了光盤驅動步進電機的軸承磨損模型,并用試驗結果確定軸承磨損模型的常數;Chin-Chung Wei 等人[17] 研究了滾珠絲杠副的預載荷對滾道接觸面微凸體磨損率與接觸面相對速度、工作行程關系的影響。
上述研究在高速精密滾珠絲杠副力學特性與磨損關系方面還不成熟,有關研究成果較少并不夠完整。本文基于Archard 模型的增量形式,分析了滾珠絲杠副運轉過程中的接觸變形和接觸角的變化,同時考慮了軸向載荷、離心力和陀螺力矩的作用,建立了滾珠磨損模型,并用數值方法求出滾珠絲杠副的磨損規律。
1.理論分析
1. 1 滾珠與滾道接觸的磨損模型
滾珠絲杠副的磨損是個動態過程,涉及諸多參數。基于黏著磨損機理,根據Archard 提出的近似計算公式可以估算滾珠絲杠副的磨損量:
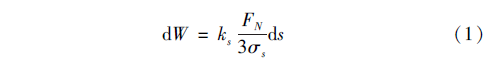

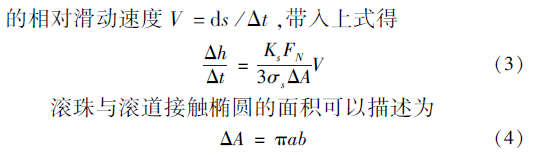
式中,橢圓參數a 和b 分別為接觸區域投影橢圓的長半軸和短半軸。
設Fa 為施加于滾珠絲桿副螺母上軸向力Fa ,則根據幾何關系有

式(6)為滾珠與滾道接觸的磨損模型。下面結合Hertz 彈性接觸特性和運動學分析求解滾珠與絲杠滾道、滾珠與螺母滾道接觸點的變形、接觸角和相對滑動速度。
1. 2 接觸面的變形
根據Hertz 彈性接觸理論,兩物體接觸點在法向力FN 作用下產生的接觸橢圓尺寸及接觸變形為[19] :

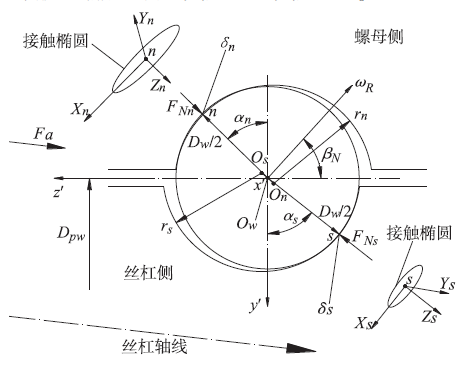
圖1 滾珠與滾道接觸示意圖

絲杠滾道表面與滾珠接觸點的兩個主曲率分別為:
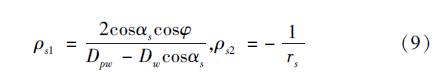
螺母滾道表面與滾珠接觸點的兩個主曲率分別為:
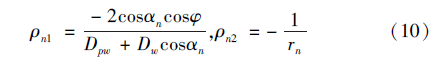
滾珠與絲杠及螺母滾道接觸點的曲率和分別為:
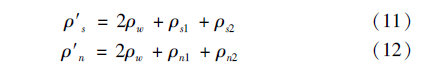

在滾珠與螺母接觸處:

1. 3 加載時接觸角的變化
滾珠高速旋轉時受到離心力和陀螺力矩作用,滾珠中心、絲杠和螺母滾道曲率中心的相對位置也會發生變化,使得滾珠與絲杠滾道、滾珠與螺母滾道的接觸角發生改變。

圖2 滾珠中心和滾道曲率中心的位置


根據幾何關系,可以得到:
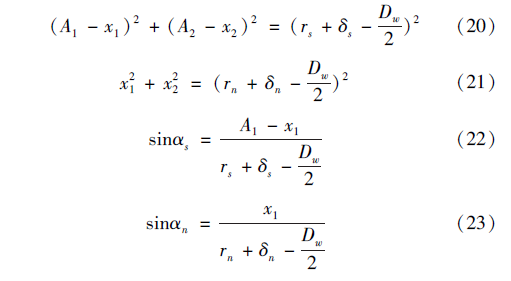

1. 4 滾珠的力平衡方程
滾珠旋轉時受到的接觸點法向力、摩擦力以及離心力等近似在一個平面內,如果忽略其它方向很小的摩擦力,則如圖3 所示。其中鋼制滾珠旋轉時產生的離心力

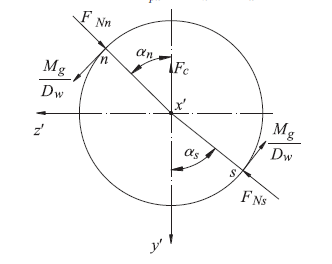
圖3 滾珠受力示意圖


式中, K 為滾珠與絲杠和螺母之間的接觸剛度系數,可由結構參數計算求出
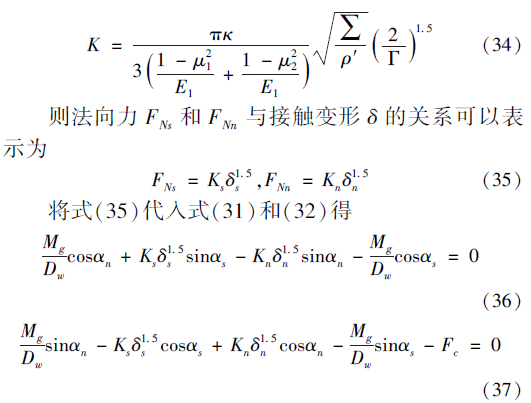


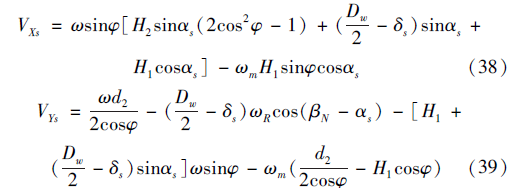
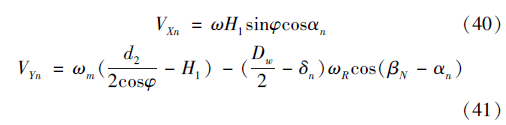

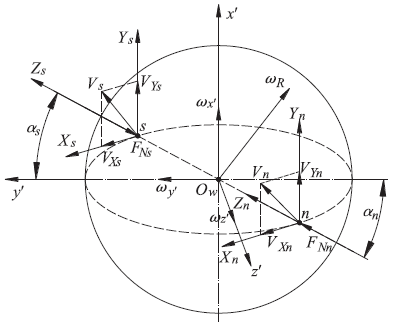
圖4 滾珠與絲杠和螺母接觸點的相對滑動速度
1. 6 磨損的理論計算




則滾珠絲桿副運行后螺母相對于絲杠的軸向位移為
2.實驗驗證
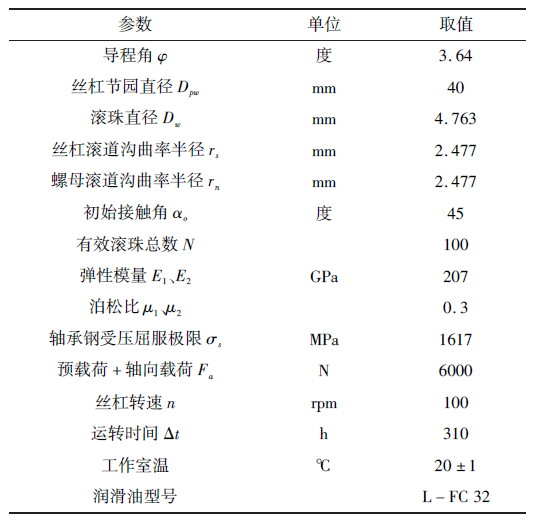
下面根據上述模型以某一型號滾珠絲桿副為例進行理論計算與試驗對比,其結構參數和運行工況條件如表1 所示。為了得到理想的載荷狀態,本試驗在自上而下的立式結構試驗臺上進行,借助施加在試驗臺下方的配重塊模擬軸向載荷的施加[20]
表1 滾珠絲杠副結構參數和運行工況
在磨損試驗的前期,新的樣件處于磨合期,試驗測量值起伏變化較大。在試驗時,先將用于測試的滾珠絲杠副磨合50h,使其進入穩定運行狀態;然后,選取磨合后的穩定運行階段的磨損量進行模型計算與試驗對比分析,并在50 ~300h 的時間段內每隔50h 測量一次有效行程變動量,用有效行程變動量表示滾珠絲桿誤差和測量偏差的干擾,試驗采用三根滾珠絲杠副按同一工況條件運行后取平均值。我們將試驗運行到第50h 的有效行程變動量測量值作為初始磨損量基準值,則此后各階段的有效行程變動量測量值與基準值之差就是相對磨損量的測量值,得到磨損量隨時間的變化規律如表2 所示結果。圖5 為滾珠絲杠副磨損量的實測值與理論計算值對比圖,從中可以看出,在本次試驗的50 ~300h 階段內,滾珠絲杠副磨損量的實測值與理論計算值的變化趨勢基本一致,當試驗時間大于300h 后磨損量的實測值明顯增大。
表2 滾珠絲杠副磨損量的實測值與理論計算值
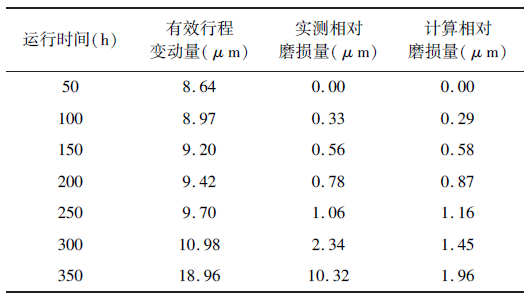
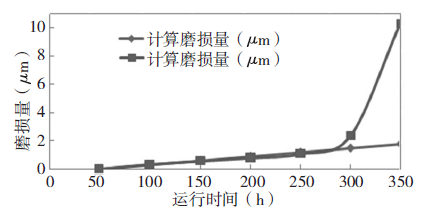
圖5 滾珠絲杠副磨損量的實測值與理論計算值對比
由于本文的理論模型是根據黏著磨損機理建立的,試驗證明,計算的磨損理論值與實測值在黏著磨損階段吻合較好,表明磨損模型準確可靠。試驗也表明,在滾珠絲杠副工作初期,發生黏著磨損的可能性較大;隨著磨損發展,磨損過程中剝落的磨屑與表面的相對運動又會加劇滾珠絲杠副的磨損,使滾珠絲杠副磨損量明顯增大。
3.結論
本文在滾珠與絲杠和螺母接觸點的變形分析的基礎上,考慮了加載時接觸角的變化和接觸點的相對滑動速度的影響,基于黏著磨損機理建立了滾珠絲杠副的磨損模型,推導出磨損后螺母相對絲杠的軸向位移。對比試驗的實測值較好地驗證了理論模型的計算結果,所建立的滾珠絲杠副磨損模型能夠反映黏著磨損階段的實際磨損變化規律。在滾珠絲杠副工作初期主要發生黏著磨損,隨著磨損發展,剝落的磨屑會誘發磨料磨損,加劇滾珠絲杠的磨損。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com





