曲面綜合法弧齒錐齒輪加工參數(shù)計(jì)算
2016-9-13 來(lái)源：河南科技大學(xué)機(jī)電工程學(xué)院 作者：魏冰陽(yáng) 鄧效忠 仝昂鑫 楊建軍
摘要：針對(duì)現(xiàn)有弧齒錐齒輪加工參數(shù)計(jì)算方法，接觸點(diǎn)綜合紛繁復(fù)雜的問(wèn)題，提出ease．off曲面綜合法。從微分幾何學(xué)出發(fā)，給出二階密切曲面的定義及其構(gòu)造方法；在二階精度范圍內(nèi)，密切曲面與原有曲面具有相同的微分幾何屬性，從而可以替代原有的曲面分析。通過(guò)弧齒錐齒輪加工的產(chǎn)成模型，構(gòu)造大小輪共軛齒面的ease．off差齒面，利用ease．off差齒面的密切曲面完整地拓?fù)潺X面接觸區(qū)；利用齒面接觸區(qū)的可控參數(shù)綜合確定小輪齒面的接觸參數(shù)，進(jìn)而通過(guò)數(shù)值優(yōu)化方法求解小輪的加工參數(shù)。籍助ease-off密切曲面進(jìn)行了嚙合仿真，完整呈現(xiàn)了齒面接觸區(qū)大小形狀、接觸路徑方向、拋物線失切量等輪齒嚙合信息。所提出的方法適宜于數(shù)值方法，基于齒面接觸區(qū)的完整性，實(shí)現(xiàn)了齒面嚙合性能較好控制。
關(guān)鍵詞：二次曲面；輪齒接觸分析：弧齒錐齒輪；差齒面
0前言
弧齒錐齒輪在機(jī)械動(dòng)力傳輸領(lǐng)域具有廣泛的應(yīng)用，其嚙合理論和制造技術(shù)一直是各國(guó)專家學(xué)者研究的熱點(diǎn)。20世紀(jì)90年代起，隨著計(jì)算機(jī)數(shù)值計(jì)算方法的應(yīng)用，弧齒錐齒輪嚙合性能預(yù)控理論和設(shè)計(jì)技術(shù)得到快速的發(fā)展。LITIVIN等[1-3]發(fā)展了“局部綜合”法，預(yù)置在參考點(diǎn)二階接觸參數(shù)，以期對(duì)輪齒傳動(dòng)誤差和齒面印痕進(jìn)行控制。吳訓(xùn)成等[4-6]發(fā)展了“主動(dòng)設(shè)計(jì)”，通過(guò)預(yù)置傳動(dòng)規(guī)律，接觸線方向修形，達(dá)到對(duì)齒面的嚙合性能預(yù)控的目的。周凱紅等[7-8]發(fā)展了基于預(yù)定嚙合特性的點(diǎn)嚙合齒面設(shè)
計(jì)方法。SIMON等[9-10]發(fā)展了弧齒錐齒輪加工參數(shù)的優(yōu)化算法。上述方法均是把曲面嚙合化為點(diǎn)接觸參數(shù)，通過(guò)接觸點(diǎn)參數(shù)的綜合實(shí)現(xiàn)對(duì)弧齒錐齒輪接觸性能的主動(dòng)控制。但點(diǎn)接觸參數(shù)綜合在對(duì)接觸點(diǎn)的矢量、曲率參數(shù)計(jì)算時(shí)，紛繁復(fù)雜，多數(shù)情況不適合數(shù)值方法計(jì)算，更不便齒面重構(gòu)、反求與誤差修正技術(shù)的應(yīng)用。
鑒于上述加工參數(shù)計(jì)算、嚙合仿真方法的不足之處，本文擬提出一種曲面綜合法，基于齒面接觸過(guò)程的完整性，通過(guò)ease．off差齒面的密切曲面拓?fù)浣佑|區(qū)，實(shí)現(xiàn)對(duì)齒面接觸性能的預(yù)控。從微分幾何學(xué)出發(fā)，給出二階密切曲面的定義及拓?fù)浞椒ǎ蕝?shù)的數(shù)值化方法；通過(guò)弧齒錐齒輪加工的產(chǎn)成模型，構(gòu)造ease．off差齒面的密切曲面，通過(guò)密切曲面拓?fù)洹⒔佑|參數(shù)綜合確定小輪齒面的接觸參數(shù)，進(jìn)而通過(guò)數(shù)值方法求解小輪的加工參數(shù)，最后借助密切曲面完成嚙合仿真。
1、二階密切曲面
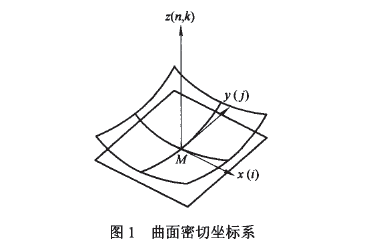
設(shè)有一個(gè)Σ2類曲面(至少存在2階以上連續(xù)微商)，在它上面的一點(diǎn)M處取坐標(biāo)系(Mxyz)，如圖1所示，X、Y軸在M點(diǎn)的切平面上，z則在M點(diǎn)的法線刀方向。若曲面Σ2在該坐標(biāo)系中的方程式為
那么，由微分幾何學(xué)可以知道【ll】，第1I基本形式為
顯然這是是一個(gè)關(guān)于(dx，dy)的二次型。
第1I基本形式近似地等于曲面與切平面的有向距離的兩倍，即
由于z軸與M點(diǎn)的法線方向一致，則式(3)表示了z軸的坐標(biāo)。在小領(lǐng)域內(nèi)可以用X代替dx，Y代替妙。所以，在M點(diǎn)的鄰域可得到如下近似式
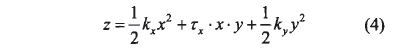
式中 ，
別表示x方向(dy=0)和y方向(dx=0)的法曲率、短程撓率。當(dāng)合理選取x、y方向，可以使 
，這時(shí)
為Σ 2曲面主曲率，X、Y為其主方向。這時(shí)曲面方程式(4)變?yōu)?/font>
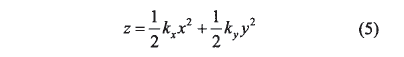
式(4)、(5)表示的曲面Σd和原曲面Σ2在二階項(xiàng)上是一致的，它們有相同的曲率參數(shù) 
。因此，把Σd為Σ2的二階密切曲面。它們?cè)谌我夥较蛏隙加邢嗤姆ㄇ始岸坛虛下省?/font>
。因此，把Σd為Σ2的二階密切曲面。它們?cè)谌我夥较蛏隙加邢嗤姆ㄇ始岸坛虛下省?/font> 由于，曲面在正常點(diǎn)的鄰域中總可以有式(1)形式的參數(shù)表示，所以總存在一張二次曲面形如式(4)，而且當(dāng)且僅當(dāng)它們具有相同的曲率參數(shù)。因此，這一論述可作為微分幾何的定理給出：
對(duì)于Σ2類曲面在正常點(diǎn)的鄰域內(nèi)，總存在一張與其相切的二次曲面，當(dāng)且僅當(dāng)它們具有相同的曲率參數(shù)。
由上述分析可以知道，對(duì)于Σ2類曲面小鄰域內(nèi)可以由二階密切曲面代替。本文利用該原理實(shí)施弧齒錐齒輪產(chǎn)成曲面的綜合、加工參數(shù)的計(jì)算及分析。
2、弧齒錐齒輪的產(chǎn)成模型
2．1大輪齒面易產(chǎn)成及其方程
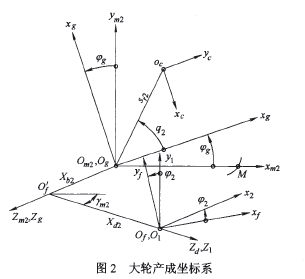
弧齒錐齒輪大輪加工一般采用雙面滾切法，加工參數(shù)一般有一致的計(jì)算方法。用如圖2所示的坐標(biāo)系描述大輪齒面的產(chǎn)成。刀盤坐標(biāo)系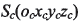 
位于瑤臺(tái)坐標(biāo)系
第一象限，繞z軸旋轉(zhuǎn)，Sg初始位置與機(jī)床坐標(biāo)系
重合，其任意瞬時(shí)相對(duì)于
轉(zhuǎn)角
，則大輪相應(yīng)的產(chǎn)成轉(zhuǎn)角為
。其余參數(shù)
為輪坯安裝角(等于大輪根錐角)，
為軸向輪位修正值。根據(jù)嚙合方程可推得
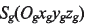位于瑤臺(tái)坐標(biāo)系第一象限，繞z軸旋轉(zhuǎn)，Sg初始位置與機(jī)床坐標(biāo)系 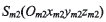重合，其任意瞬時(shí)相對(duì)于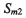轉(zhuǎn)角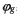，則大輪相應(yīng)的產(chǎn)成轉(zhuǎn)角為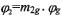。其余參數(shù)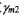為輪坯安裝角(等于大輪根錐角)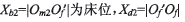，為軸向輪位修正值。根據(jù)嚙合方程可推得
2．2共軛小輪齒面Σl
利用大輪齒面產(chǎn)成小輪齒面為包絡(luò)原理，假設(shè)大小輪嚙合的初始角度為庇o、咖o，則任意嚙合位置大小輪之間的轉(zhuǎn)角的關(guān)系為
2．3數(shù)值微分求共軛小輪的曲率參數(shù)
給定大輪齒面Σ2上參考點(diǎn)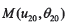
的曲面參數(shù)
，并給定微分
增量，利用上述式(1)～(9)運(yùn)算，求數(shù)值微分
即
的曲面參數(shù)，并給定微分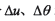增量，利用上述式(1)～(9)運(yùn)算，求數(shù)值微分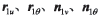即
3 、Ease．off曲面綜合
對(duì)共軛小輪齒面Σ 1修形，在計(jì)算點(diǎn)M領(lǐng)域內(nèi)必然能夠構(gòu)造一個(gè)在M點(diǎn)相切的其余鄰域失切的小輪修形齒面，稱為切觸齒面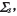
，相應(yīng)的主方向、主曲率記作
，相應(yīng)的主方向、主曲率記作
3．1齒面接觸區(qū)拓?fù)?/font>
在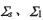
之間沿法線方向構(gòu)造差曲面稱為ease．off曲面
反映了共軛齒面的失切量，該曲面在點(diǎn)M領(lǐng)域可以用形如式(5)的密切曲面代替
之間沿法線方向構(gòu)造差曲面稱為ease．off曲面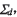反映了共軛齒面的失切量，該曲面在點(diǎn)M領(lǐng)域可以用形如式(5)的密切曲面代替
4、小輪齒面五加工參數(shù)的計(jì)算
4．1小輪產(chǎn)成模型
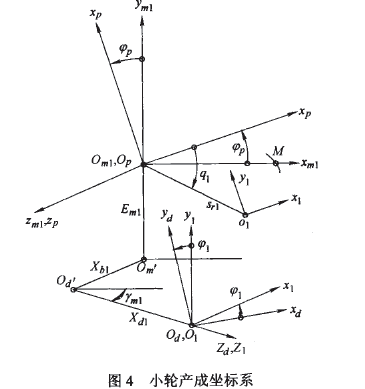
根據(jù)小輪產(chǎn)成原理，建立如圖4所示的坐標(biāo)系來(lái)描述小輪的產(chǎn)成過(guò)程。刀盤坐標(biāo)系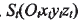
的原點(diǎn)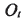
為刀盤中心，
為刀尖平面(與機(jī)床平面重合)，并與搖臺(tái)坐標(biāo)系
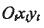為刀盤中心，為刀尖平面(與機(jī)床平面重合)，并與搖臺(tái)坐標(biāo)系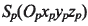固聯(lián)，且各坐標(biāo)軸對(duì)應(yīng)平行。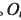
在坐標(biāo)系SP的極坐(
為角向刀位和徑向刀位。Sp初始位置與機(jī)床坐標(biāo)系
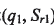在坐標(biāo)系SP的極坐(為角向刀位和徑向刀位。Sp初始位置與機(jī)床坐標(biāo)系
4．2小輪加工參數(shù)計(jì)算與仿真
4．2．1 小輪的ant參數(shù)的數(shù)值求解
利用前述第2．3節(jié)的數(shù)值微分方法，對(duì)式(20)求數(shù)值微分，計(jì)算小輪的主方向、主曲率，同時(shí)將徑矢、法矢統(tǒng)一記作
上述方程是含有小輪加工參數(shù)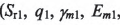
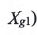,刀盤參數(shù)
曲紋坐標(biāo)參數(shù)
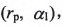,刀盤參數(shù)曲紋坐標(biāo)參數(shù)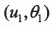的9個(gè)非線性方程組。通過(guò)求解該方程組可確定小輪的加工參數(shù)。
在求解之前，有些參數(shù)是可以首先確定的，輪坯安裝角肋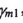
，刀盤壓力角
，刀盤壓力角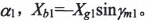所以實(shí)際求解的參數(shù)為6個(gè)。
式(22)的解的初值和取值范圍是比較容易確定的，所以式(22)適宜用優(yōu)化的方法求解。本文采用非線性約束優(yōu)化求解的辦法，利用Matlab優(yōu)化函數(shù)fmincon完成了一個(gè)實(shí)例計(jì)算，結(jié)果如表1所示。
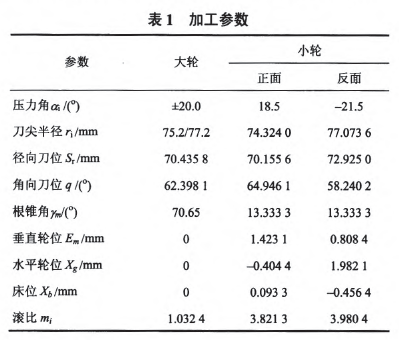
4．2．2 嚙合仿真
為了驗(yàn)證表l加工參數(shù)計(jì)算的準(zhǔn)確性，通過(guò)構(gòu)建ease—off差齒面進(jìn)行接觸仿真，結(jié)果如圖5所示ease-off為二次凸曲面，反映齒面接觸呈局部共軛特性，齒面兩端離差在0．04---0．05 mm之間。通過(guò)對(duì)
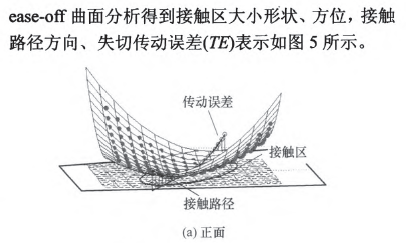
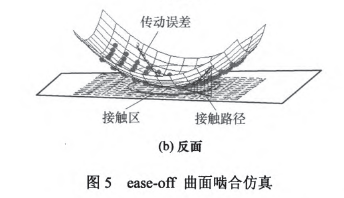
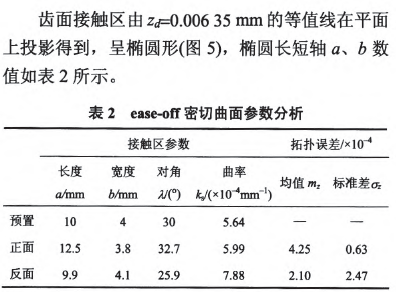
5 、結(jié)論
(1)針對(duì)現(xiàn)有弧齒錐齒輪N-r參數(shù)計(jì)算方法，接觸點(diǎn)綜合紛繁復(fù)雜，不適宜數(shù)值方法計(jì)算的不足之處，給出了ease．off曲面綜合法。從微分幾何學(xué)出發(fā)，給出了二階密切曲面的定義及其拓?fù)浞椒ǎ辉诙A精度范圍內(nèi)，密切曲面與原有曲面具有相同的微分幾何屬性，從而可以替代原有的曲面分析。
(2)通過(guò)弧齒錐齒輪加工的產(chǎn)成模型，構(gòu)造了ease—off密切曲面，拓?fù)潺X面接觸區(qū)；通過(guò)曲面綜合確定了小輪齒面的接觸參數(shù)，利用數(shù)值方法求解出小輪加工參數(shù)，借助ease．off密切曲面完成了齒面的嚙合真本文所提出的曲面綜合法適合數(shù)值計(jì)算，能夠主控齒面接觸區(qū)，預(yù)置參數(shù)能動(dòng)性較好，嚙合仿真呈現(xiàn)了輪齒接觸的完整信息。
投稿箱：
如果您有機(jī)床行業(yè)、企業(yè)相關(guān)新聞稿件發(fā)表，或進(jìn)行資訊合作，歡迎聯(lián)系本網(wǎng)編輯部， 郵箱：skjcsc@vip.sina.com
如果您有機(jī)床行業(yè)、企業(yè)相關(guān)新聞稿件發(fā)表，或進(jìn)行資訊合作，歡迎聯(lián)系本網(wǎng)編輯部， 郵箱：skjcsc@vip.sina.com
更多相關(guān)信息
業(yè)界視點(diǎn)
| 更多
行業(yè)數(shù)據(jù)
| 更多
- 2025年1月 新能源汽車銷量情況
- 2024年12月 新能源汽車產(chǎn)量數(shù)據(jù)
- 2024年12月 基本型乘用車（轎車）產(chǎn)量數(shù)據(jù)
- 2024年12月 軸承出口情況
- 2024年12月 分地區(qū)金屬切削機(jī)床產(chǎn)量數(shù)據(jù)
- 2024年12月 金屬切削機(jī)床產(chǎn)量數(shù)據(jù)
- 2024年11月 金屬切削機(jī)床產(chǎn)量數(shù)據(jù)
- 2024年11月 分地區(qū)金屬切削機(jī)床產(chǎn)量數(shù)據(jù)
- 2024年11月 軸承出口情況
- 2024年11月 基本型乘用車（轎車）產(chǎn)量數(shù)據(jù)
- 2024年11月 新能源汽車產(chǎn)量數(shù)據(jù)
- 2024年11月 新能源汽車銷量情況
- 2024年10月 新能源汽車產(chǎn)量數(shù)據(jù)
博文選萃
| 更多
- 機(jī)械加工過(guò)程圖示
- 判斷一臺(tái)加工中心精度的幾種辦法
- 中走絲線切割機(jī)床的發(fā)展趨勢(shì)
- 國(guó)產(chǎn)數(shù)控系統(tǒng)和數(shù)控機(jī)床何去何從？
- 中國(guó)的技術(shù)工人都去哪里了？
- 機(jī)械老板做了十多年，為何還是小作坊？
- 機(jī)械行業(yè)最新自殺性營(yíng)銷，害人害己！不倒閉才
- 制造業(yè)大逃亡
- 智能時(shí)代，少談點(diǎn)智造，多談點(diǎn)制造
- 現(xiàn)實(shí)面前，國(guó)人沉默。制造業(yè)的騰飛，要從機(jī)床
- 一文搞懂?dāng)?shù)控車床加工刀具補(bǔ)償功能
- 車床鉆孔攻螺紋加工方法及工裝設(shè)計(jì)
- 傳統(tǒng)鉆削與螺旋銑孔加工工藝的區(qū)別